


Next: From Bayesian inference to
Up: Inferring numerical values of
Previous: Predictive distributions
Hierarchical modelling and hyperparameters
As we have seen in the previous section,
it is often desirable to include in a probabilistic model one's
uncertainty in various aspects of a pdf.
This is a natural feature of the Bayesian methods,
due to the uniform approach to deal with uncertainty
and from which powerful analysis tools are derived.
This kind of this modelling is called
hierarchical because the characteristics
of one pdf are controlled by another pdf.
All uncertain parameters from which the pdf
depends are called hyperparameter.
An example of use of hyperparameter is described in
Sect. 8.3 in which the
prior to infer 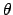 in a binomial model are shown to be controlled
by the parameters of a Beta distribution.
in a binomial model are shown to be controlled
by the parameters of a Beta distribution.
As an example of practical importance, think of
the combination of experimental results in the presence
of outliers, i.e. of data points which are
somehow in mutual disagreement. In this case the combination
rule given by Eqs. (30)-(32),
extended to many data points, produces unacceptable conclusions.
A way of solving the problem (Dose and von der Linden 1999,
D'Agostini 1999b) is to model a scepticism about the quoted
standard deviations of the experiments, introducing
a pdf 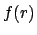 , where
, where 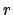 is a rescaling factor of the
standard deviation. In this way the
is a rescaling factor of the
standard deviation. In this way the 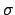 's that enter
the r.h.s. of Eqs. (30)-(32)
are hyperparameters of the problem.
An alternative approach,
also based on hierarchical modelling, is shown in (Fröhner 2000).
For a more complete introduction to the subject see e.g.
(Gelman et al 1995).
's that enter
the r.h.s. of Eqs. (30)-(32)
are hyperparameters of the problem.
An alternative approach,
also based on hierarchical modelling, is shown in (Fröhner 2000).
For a more complete introduction to the subject see e.g.
(Gelman et al 1995).



Next: From Bayesian inference to
Up: Inferring numerical values of
Previous: Predictive distributions
Giulio D'Agostini
2003-05-13
![]() , where
, where ![]() is a rescaling factor of the
standard deviation. In this way the
is a rescaling factor of the
standard deviation. In this way the ![]() 's that enter
the r.h.s. of Eqs. (30)-(32)
are hyperparameters of the problem.
An alternative approach,
also based on hierarchical modelling, is shown in (Fröhner 2000).
For a more complete introduction to the subject see e.g.
(Gelman et al 1995).
's that enter
the r.h.s. of Eqs. (30)-(32)
are hyperparameters of the problem.
An alternative approach,
also based on hierarchical modelling, is shown in (Fröhner 2000).
For a more complete introduction to the subject see e.g.
(Gelman et al 1995).