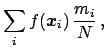Next: Rejection sampling
Up: Monte Carlo methods
Previous: Monte Carlo methods
The easy part of the Bayesian approach is to
write down the
un-normalized distribution of the parameters
(Sect. 5.10), given the prior and the likelihood.
This is simply
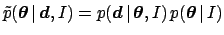 .
The difficult task is to normalize this function and to calculate all
expectations in which we are interested, such as
expected values, variances, covariances
and other moments. We might also want to get marginal distributions,
credibility intervals (or hypervolumes) and so on.
As is well-known, if we were able to sample the posterior
(even the un-normalized one),
i.e. to generate points of the parameter space according to their probability,
we would have solved the problem, at least
approximately.
For example, the one-dimensional histogram of parameter
.
The difficult task is to normalize this function and to calculate all
expectations in which we are interested, such as
expected values, variances, covariances
and other moments. We might also want to get marginal distributions,
credibility intervals (or hypervolumes) and so on.
As is well-known, if we were able to sample the posterior
(even the un-normalized one),
i.e. to generate points of the parameter space according to their probability,
we would have solved the problem, at least
approximately.
For example, the one-dimensional histogram of parameter 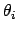 would represent its marginal and would allow the calculation of
would represent its marginal and would allow the calculation of
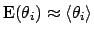 ,
,
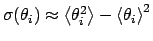 and of
probability intervals (
and of
probability intervals (
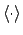 in the previous formulae stand for arithmetic
averages of the MC sample).
in the previous formulae stand for arithmetic
averages of the MC sample).
Let us consider the probability function
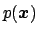 of
the discrete variables
of
the discrete variables
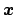 and a function
and a function
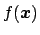 of which we want to evaluate the expectation over the distribution
of which we want to evaluate the expectation over the distribution
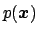 . Extending the one-dimensional formula
of Tab. 1
to
. Extending the one-dimensional formula
of Tab. 1
to 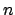 dimension
we have
dimension
we have
where the summation in Eq. (109) is over the components,
while the summation in Eq. (110) is over possible points
in the 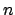 -dimensional space of the variables.
The result is the same.
-dimensional space of the variables.
The result is the same.
If we are able to sample a large number of points 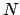 according to the
probability function
according to the
probability function
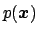 , we expect
each point to be generated
, we expect
each point to be generated 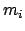 times.
The average
times.
The average
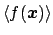 , calculated from the sample as
, calculated from the sample as
(in which the index is named 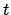 as a reminder that this is a sum over
a `time' sequence) can also be rewritten as
as a reminder that this is a sum over
a `time' sequence) can also be rewritten as
just grouping together the outcomes giving the same
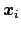 .
For a very large
.
For a very large 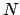 , the ratios
, the ratios 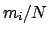 are expected to be
`very close' to
are expected to be
`very close' to
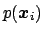 (Bernoulli's theorem),
and thus
(Bernoulli's theorem),
and thus
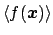 becomes a good approximation
of
becomes a good approximation
of
![$\mbox{E}[f({\mbox{\boldmath$x$}})]$](img508.png) . In fact, this approximation can be
good (within tolerable errors) even if not all
. In fact, this approximation can be
good (within tolerable errors) even if not all 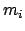 are large and, indeed,
even if many of them are null.
Moreover, the same procedure can be
extended to the continuum, in which case `all points' (
are large and, indeed,
even if many of them are null.
Moreover, the same procedure can be
extended to the continuum, in which case `all points' (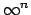 )
can never be sampled.
)
can never be sampled.
For simple distributions there are well-known standard techniques
for generating pseudo-random numbers starting from pseudo-random numbers
distributed
uniformly between 0 and 1
(computer libraries are available for sampling
points according to the most common
distributions).
We shall not enter into
these basic techniques, but will concentrate instead on
the calculation of expectations in more complicated cases.



Next: Rejection sampling
Up: Monte Carlo methods
Previous: Monte Carlo methods
Giulio D'Agostini
2003-05-13
![]() of
the discrete variables
of
the discrete variables
![]() and a function
and a function
![]() of which we want to evaluate the expectation over the distribution
of which we want to evaluate the expectation over the distribution
![]() . Extending the one-dimensional formula
of Tab. 1
to
. Extending the one-dimensional formula
of Tab. 1
to ![]() dimension
we have
dimension
we have
![]() according to the
probability function
according to the
probability function
![]() , we expect
each point to be generated
, we expect
each point to be generated ![]() times.
The average
times.
The average
![]() , calculated from the sample as
, calculated from the sample as