What do we learn by a second test?
Let us imagine that the same individual undergoes
a second test and that
the result is again Positive. How should we update
our believes that this individual is infected,
in the light of the second observation?
The first idea would be to apply Bayes' rule
in sequence, thus getting an overall Bayes' Factor
of
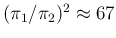 that, multiplied by the initial
odds of
that, multiplied by the initial
odds of 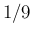 , would give posterior odds of 7.4, or a
probability of being infected of 88%, still far from a
practical certainty. But the real question is if we can
apply twice the same kind of test to the same person.
It is easy to understand that the multiplication of the Bayes' factors
assumes (stochastic) independence among them.
In fact, according to probability theory we have to
replace now Eq. (
, would give posterior odds of 7.4, or a
probability of being infected of 88%, still far from a
practical certainty. But the real question is if we can
apply twice the same kind of test to the same person.
It is easy to understand that the multiplication of the Bayes' factors
assumes (stochastic) independence among them.
In fact, according to probability theory we have to
replace now Eq. (![[*]](crossref.png) ) by
) by
having indicated by
Pos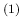 and
Pos
and
Pos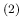 the two outcomes.
Numerator and denominator of the Bayes' Factor
are then
the two outcomes.
Numerator and denominator of the Bayes' Factor
are then
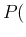 Pos Pos Pos Pos Inf Inf |
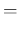 |
 Pos Pos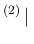 Pos Pos Inf Inf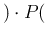 Pos Pos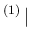 Inf Inf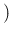 |
|
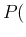 Pos Pos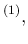 Pos Pos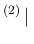 NoInf NoInf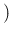 |
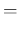 |
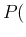 Pos Pos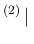 Pos Pos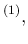 NoInf NoInf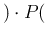 Pos Pos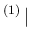 NoInf NoInf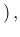 |
|
which can be rewritten as
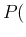 Pos Pos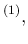 Pos Pos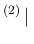 Inf Inf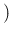 |
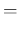 |
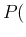 Pos Pos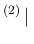 Inf Inf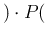 Pos Pos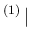 Inf Inf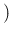 |
|
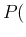 Pos Pos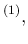 Pos Pos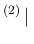 NoInf NoInf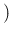 |
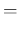 |
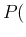 Pos Pos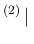 NoInf NoInf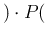 Pos Pos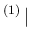 NoInf NoInf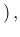 |
|
and therefore we can factorize the two Bayes' factors,
only if the two test results are independent.
But this is far from being obvious. If the test response
depends on something one has in the blood, different from
the virus one is searching for,
a second test of the same kind will most likely give the
same result.
![[*]](crossref.png) ) by
) by