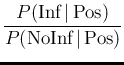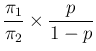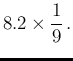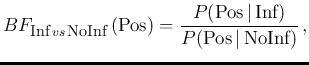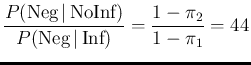Initial odds, final odds and Bayes' factor
Let us go again to the above formulae, which
we rewrite in different ways in order to get some insights on what
is going on.
Before the test, if no other information is available,
the initial odds Infected vs Not Infected are
given by
equal to 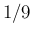 for our reference value of
for our reference value of 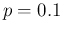 .
After the test has resulted in Positive
the new probability of Infected is given by Eq. (
.
After the test has resulted in Positive
the new probability of Infected is given by Eq. (![[*]](crossref.png) ).
The corresponding probability of Not Infected is given by
a fraction that has the same denominator but
).
The corresponding probability of Not Infected is given by
a fraction that has the same denominator but
 Pos
Pos NoInf
NoInf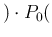 NoInf
NoInf as numerator.
The final odds
are then given by
as numerator.
The final odds
are then given by
Using our numerical values, we get
The effect of the test resulting in Positive
has been to modify the initial
odds by the factor
known as Bayes' Factor.13In our case this factor is equal to
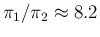 .
This means that after a person has been tagged as Positive,
the odds Infected vs Not Infected have increased by this factor.
But since the initial odds were
.
This means that after a person has been tagged as Positive,
the odds Infected vs Not Infected have increased by this factor.
But since the initial odds were 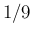 ,
the final odds are just below 1, that is about 1-to-1, or 50-50.
,
the final odds are just below 1, that is about 1-to-1, or 50-50.
In the same way we can define the
Bayes Factor Not Infected vs Infected
in the case of a negative result:
This is the reason why, for a hypothetical proportion
of infectees in the population of 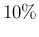 , a negative result
makes one practically sure to be not infected. The
initial odds of 9-to-1 are multiplied by a factor 44, thus
reaching 396, about 400-to-1, resulting into a probability
of not being infected of 396/397, or 99.75%.
, a negative result
makes one practically sure to be not infected. The
initial odds of 9-to-1 are multiplied by a factor 44, thus
reaching 396, about 400-to-1, resulting into a probability
of not being infected of 396/397, or 99.75%.
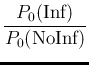
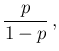
![[*]](crossref.png) ).
The corresponding probability of Not Infected is given by
a fraction that has the same denominator but
).
The corresponding probability of Not Infected is given by
a fraction that has the same denominator but