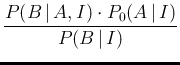- ... D'Agostini1
-
Università “La Sapienza” and INFN, Roma, Italia,
giulio.dagostini@roma1.infn.it
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Esposito2
-
Retired, alfespo@yahoo.it
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... not.1
- For example we would have started
choosing, in Italy,
the families involved in the Auditel system [15],
created with the purpose to infer the
share of television programs, on the basis of which advertisers
pay the TV channels. In general, in order to make sampling meaningful,
the selection of individuals cannot be left to a voluntary choice
that would inevitably bias the outcomes of the test campaign.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... infected 2
- In fact,
the test reported in Ref. [16]
was claimed to be sensitive both to
Immunoglobulin M (IgM), the antibody related
to a current infection,
and Immunoglobulin G (IgG) related to
a past infection [17,18].
Obviously, the effectiveness of these kind
of `serological tests' is not questioned here.
In particular, two kinds of immunoglobulins
will take some time to develop and they
are most likely characterized by decay times.
Therefore, the generic expression infected individuals
(or in short infectees)
has to be meant as the
members of the population
which hold some `property' to which the test is sensitive
at the time in which it is performed.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... `probabilities'.3
- If you are not used to attach a probability
to numbers that might have by themselves the meaning of
probability, Ref. [19] is recommended.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... intent4
- The educational
writing is an old idea that both the authors pursued in the past
(see e.g. Refs. [20,21,22]),
strongly believing in the necessity of
making the management of uncertainty a basic tenet of scholastic
(and not only) curricula.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... overlooked.5
- This problem
has been recently addressed by an article on Scientific
American [23], with arguments similar
to the simplistic one we are going to show in
Sec.
![[*]](crossref.png) , although complemented by a rather popular
visualization of the question. But we have been surprised
by the lack of
any reference to probability theory and to the Bayes' rule
in the paper.
, although complemented by a rather popular
visualization of the question. But we have been surprised
by the lack of
any reference to probability theory and to the Bayes' rule
in the paper.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... response,6
- But
we hardly believe that they only provide binary information,
of the kind Yes/No, and we wonder why a
(although slightly) more refined scale is not reported,
even discretized in a few steps, like when we rank
goods and services with stars.
Anyway, we shall not touch this question in the present paper,
but only wanted to express here our perplexity.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
infected.7
- This point is quite relevant
when the so called false positive regards some disease
with a strong social stigma (e.g. AIDS). Bad practices and negligence
in dealing with test results and ignoring the population background
caused genuine emotional suffering, heavy distress, up to suicide
attempts [30]. The same applies in forensics, where individual freedom and justice can be badly influenced
by evidence mismanagement (See Ref. [31,32] and the references there). In a less tragic context,
ignoring the role of the priors can cause bad decisions to be made
(see e.g. Ref. [33] for an application
concerning Information Security).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... population.8
- We remind that
we are not taking into account symptoms or other reasons
that would increase or decrease the
probability of a particular individual to be
infected. For example, the journalist of Ref. [16]
tells that he had `some suspicions' he could have been infected
on a plane.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....9
- Mathematically,
also negative numerator and denominator would yield
a positive value of
 , although this case makes no sense
in practice, requiring
, although this case makes no sense
in practice, requiring  smaller than
smaller than  .
Moreover, the mathematical divergence of Eq. (
.
Moreover, the mathematical divergence of Eq. (![[*]](crossref.png) )
- of no practical relevance, as we have already commented -
for
)
- of no practical relevance, as we have already commented -
for
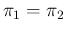 is indeed due to the fact Eq. (
is indeed due to the fact Eq. (![[*]](crossref.png) )
and (
)
and (![[*]](crossref.png) ) become then
) become then
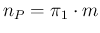 and
and
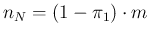 , not depending any longer on
, not depending any longer on  .
.
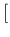 In more detail, taking
In more detail, taking
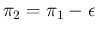 , we get
, we get
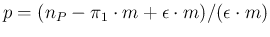 ,
diverging for
,
diverging for
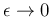 .
.![$]$](img65.png)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... rule),10
- See Appendix A for details.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... `before'11
- This usual expression, regularly used in the
literature together with the term prior,
could transmit the wrong idea of time order strictly needed,
leading to the absurdity that the Bayes' theorem could not be applied
if one did not `declare' (to a notary?) in advance her
priors. What really matters, e.g. in this specific example,
is the probability that the tested person could be infected
or not, taking into account all other information but the test result.
(We shall comment further on the meaning and the role of the priors,
in particular in Sec.
![[*]](crossref.png) .)
.)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... caption.12
- The reader might be surprised to
see plots in which
 goes up to 1, but the reason is twofold:
first,
goes up to 1, but the reason is twofold:
first,  can be also interpreted in these plots as
the purely subjective degree of belief of the expert that
the tested individual is infected, independently of the test result;
second, the aim of this paper is rather general and,
from a physicist's perspective,
can be also interpreted in these plots as
the purely subjective degree of belief of the expert that
the tested individual is infected, independently of the test result;
second, the aim of this paper is rather general and,
from a physicist's perspective,  could have the meaning
of a detector efficiency, a branching ratio in particle decays,
and whatever can be modeled by a binomial distribution.
could have the meaning
of a detector efficiency, a branching ratio in particle decays,
and whatever can be modeled by a binomial distribution.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Factor.13
- A more proper
name could be Bayes-Turing factor, or perhaps
even better Gauss-Turing factor [34], but we stick
here to the conventional name.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... certainty14
- This is what we assume, although we
are not in the position to enter into the details.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...:15
- Some clarifications are provided
in Appendix A. With reference to Eq. (A.8) there,
Eq. (
![[*]](crossref.png) ) derives from
) derives from
in which we have used a pedantic chain rule derived
from a bottom-up analysis of the second graphical model of
Fig. ![[*]](crossref.png) (the one in which
(the one in which  is unknown)
and taking into account, in the final step, that
is unknown)
and taking into account, in the final step, that
 does not depend on
does not depend on 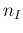 ,
which has a precise, well known value in this problem.
We can note also that
,
which has a precise, well known value in this problem.
We can note also that
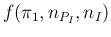 involves the continuous variable
involves the continuous variable  and the discrete values
and the discrete values 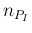 and
and 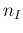 , being then strictly speaking
neither a probability function nor a probability density function,
while the meaning of each term of the chain rule
is clear from the nature (continuous or discrete) of each variable
(see Appendix A for details).
, being then strictly speaking
neither a probability function nor a probability density function,
while the meaning of each term of the chain rule
is clear from the nature (continuous or discrete) of each variable
(see Appendix A for details).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... unreasonable,16
- Nevertheless,
we shall comment in Sec.
![[*]](crossref.png) about the practical importance of using a flat prior,
because it is possible to modify the result
in a second step, `reshaping' the posterior
by personal, informative priors based on the best
knowledge of the problem, which might be different
for different experts (remember that the `prior'
does not imply time order, as remarked in
footnote
about the practical importance of using a flat prior,
because it is possible to modify the result
in a second step, `reshaping' the posterior
by personal, informative priors based on the best
knowledge of the problem, which might be different
for different experts (remember that the `prior'
does not imply time order, as remarked in
footnote ![[*]](crossref.png) ).
).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... way.17
- See Sec.
![[*]](crossref.png) for advice about the usage of mathematically convenient models.
for advice about the usage of mathematically convenient models.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... structure:18
- Our preferred vademecum of Probability
Distributions is the
homonymous app [1].
More details are given in Sec.
![[*]](crossref.png) .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... test.19
- To be fastidious,
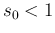 is not acceptable, because we do not believe
a priori that a test could be perfect, and therefore
is not acceptable, because we do not believe
a priori that a test could be perfect, and therefore
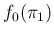 has to vanish at
has to vanish at 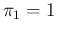 . This implies that
. This implies that
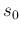 must be slightly above 1, for example 1.1. But in our case
the observation of at least one Negative would automatically
rule out
must be slightly above 1, for example 1.1. But in our case
the observation of at least one Negative would automatically
rule out 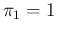 . Anyway, although this little numerical
difference is irrelevant in our case, we use
. Anyway, although this little numerical
difference is irrelevant in our case, we use 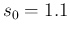 only because, since we plot priors and posteriors in
Fig.
only because, since we plot priors and posteriors in
Fig. ![[*]](crossref.png) we do not like to show a prior not vanishing at 1.
we do not like to show a prior not vanishing at 1.
 We are admittedly a bit pedantic here for
didactic purposes, but we shall be more pragmatic
later (see Sec.
We are admittedly a bit pedantic here for
didactic purposes, but we shall be more pragmatic
later (see Sec. ![[*]](crossref.png) )
and even critical about the literal use of mathematical
expressions that should instead only be employed for convenience and
cum grano salis (see Sec.
)
and even critical about the literal use of mathematical
expressions that should instead only be employed for convenience and
cum grano salis (see Sec. ![[*]](crossref.png) ).
).![$]$](img65.png)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... CLASS="MATH">
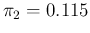 .20
.20
- If, instead, we had used
flat prior over the two parameters, we would get, by
the Laplace' rule of succession that we shall see in a while,
0.978 and 0.124. The result is identical (within rounding)
for
 and practically the same for
and practically the same for  , because
with hundreds of trials the inference is dominated by the data.
(We insist in being fastidiously pedantic because of the didactic
aim of this paper. For more
on priors, and for the practical importance of routinely
using a flat one, see Sec.
, because
with hundreds of trials the inference is dominated by the data.
(We insist in being fastidiously pedantic because of the didactic
aim of this paper. For more
on priors, and for the practical importance of routinely
using a flat one, see Sec. ![[*]](crossref.png) .)
.)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....21
- In
the case of a uniform prior, i.e.
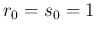 , we get
, we get
known as Laplace's rule of succession. In particular,
for large values of 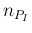 and
and 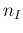 ,
,
 Pos
Pos Inf
Inf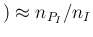 :
more frequently past tests applied to surely
infected individuals
resulted in Positive,
more probably we have to expect a positive outcome of
a new test of the same kind applied
to an infected individual.
:
more frequently past tests applied to surely
infected individuals
resulted in Positive,
more probably we have to expect a positive outcome of
a new test of the same kind applied
to an infected individual.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....22
- In principle
 and
and  are not really independent, because
they might depend on how the test `technology' has been optimized,
and it could be easily that aiming to
reach high `sensitivity' affects `specificity'. But
with the information available to us we can only take them
independent, each one obtained by the number of positives
and negatives observed in, hopefully, well controlled samples
of infected and not infected individuals.
are not really independent, because
they might depend on how the test `technology' has been optimized,
and it could be easily that aiming to
reach high `sensitivity' affects `specificity'. But
with the information available to us we can only take them
independent, each one obtained by the number of positives
and negatives observed in, hopefully, well controlled samples
of infected and not infected individuals.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Carlo,23
- The rational
is quite easy to understand, starting e.g.
from Eq. (
![[*]](crossref.png) ) and remembering that
) and remembering that
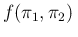 d
d d
d represents the
infinitesimal probability d
represents the
infinitesimal probability d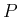 that
that  and
and  occur in the infinitesimal cell
d
occur in the infinitesimal cell
d d
d .
We can discretize the plane
.
We can discretize the plane
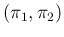 in
in 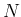 cells and indicate by
cells and indicate by 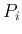 the probability that
a point of
the probability that
a point of  and
and  falls inside it.
Equation (
falls inside it.
Equation (![[*]](crossref.png) ) can be approximated
as
) can be approximated
as
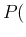 Inf Inf Pos Pos |
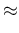 |
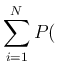 Inf Inf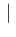 Pos Pos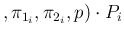 |
|
| |
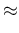 |
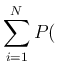 Inf Inf Pos Pos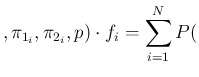 Inf Inf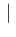 Pos Pos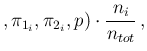 |
|
in which we have approximated each 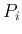 by its
expected relative frequency of occurrence
by its
expected relative frequency of occurrence
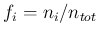 (Bernoulli's theorem). As one can see, we have approximated
the integral by a weighted average, in which the
cells in the plane that are expected to be more probable count
more. In reality we do not even need to subdivide the plane into cells.
We just extract at random
(Bernoulli's theorem). As one can see, we have approximated
the integral by a weighted average, in which the
cells in the plane that are expected to be more probable count
more. In reality we do not even need to subdivide the plane into cells.
We just extract at random  and
and  in the plane, according
to their probability distributions, calculate
in the plane, according
to their probability distributions, calculate
 Inf
Inf Pos
Pos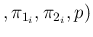 at each point and
calculate the average. When we consider a very large
at each point and
calculate the average. When we consider a very large  , then
we expect that the average will not differ much from the integral.
, then
we expect that the average will not differ much from the integral.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... integral.24
- A similar effect happens in evaluating
the contribution of systematics on measured physical quantity.
If the dependence of the `influence factor' [29]
is almost linear, then the `central value' is practically not affected,
and only its `standard uncertainty' increases.
 But in our case
we are only interested on its `central value', that is e.g.
the result of the integrals of
Eqs. (
But in our case
we are only interested on its `central value', that is e.g.
the result of the integrals of
Eqs. (![[*]](crossref.png) )-(
)-(![[*]](crossref.png) ).
).![$]$](img65.png)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
independent.25
- The question could be
a bit more sophisticated, and we have already commented
in footnote
![[*]](crossref.png) on the possible dependency of
on the possible dependency of  and
and  .
But, given the information at hand and the purpose of this
paper, this is a more than reasonable assumption.
.
But, given the information at hand and the purpose of this
paper, this is a more than reasonable assumption.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... B.126
-
One just needs to replace `p = 0.1' by
`p = rbeta(n, 3.5, 31.5)', to be placed
after n has been defined.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...tab:prob_vs_parametri.27
- The reason why
the integral over all possible values of
 gives
gives
 Inf
Inf Pos
Pos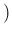 smaller than that obtained
at a fixed value of
smaller than that obtained
at a fixed value of  can be understood looking
at the solid red curve of Fig.
can be understood looking
at the solid red curve of Fig. ![[*]](crossref.png) showing
showing
 Inf
Inf Pos
Pos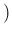 as a function of
as a function of  around
around 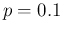 ,
indicated by the vertical dashed line. If
,
indicated by the vertical dashed line. If  has a symmetric variation
around 0.1 of
has a symmetric variation
around 0.1 of 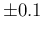 (just to make things more evident),
than
(just to make things more evident),
than
 Inf
Inf Pos
Pos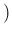 has an asymmetric variation
of
has an asymmetric variation
of
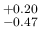 around 0.476 and therefore the Monte Carlo average
will be quite below 0.476 (but the Beta distribution
used for
around 0.476 and therefore the Monte Carlo average
will be quite below 0.476 (but the Beta distribution
used for  is skewed on the right side and therefore
there is a little compensation). For the same reason
is skewed on the right side and therefore
there is a little compensation). For the same reason
 NoInf
NoInf Neg
Neg , practically flat in that region of
, practically flat in that region of  ,
is instead rather insensitive on the exact value of
,
is instead rather insensitive on the exact value of  (unless we take unrealistic values around 0.9).
(unless we take unrealistic values around 0.9).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... link,28
- This convention is standard
in the literature, although one might object - and we agree -
that the opposite
one would have been a better choice, a solid line better representing
a deterministic link than a dashed one, but we stick to the convention.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
linearization.29
- See Sec. 6.4 of Ref. [2]
and Sec. 8.6 of Ref. [3].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... expressions:30
- The first two terms
of the r.h.s. of Eq. (
![[*]](crossref.png) ) come from
Eq. (
) come from
Eq. (![[*]](crossref.png) ), in which the precise values
), in which the precise values
 and
and  have been replaced by their expected value.
The other two terms are obtained by linearization, yielding
e.g. for the contribution due to
have been replaced by their expected value.
The other two terms are obtained by linearization, yielding
e.g. for the contribution due to  (remember that
(remember that  is, so far, a precise parameter)
is, so far, a precise parameter)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... style31
- For this question see the ISO's GUM [29].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
rounding,32
- Using the values 0.0196 and 0.0031 of
Fig.
![[*]](crossref.png) we would get 0.194.
we would get 0.194.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
linearization,33
- The contribution
to
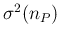 due to
due to
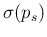 ,
evaluated by linearization, is given by
,
evaluated by linearization, is given by
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... systematics.34
- Note that this terminology is a matter
of convention and habits. From a probabilistic point of view
we just apply probability theory to all quantities with respect to
which we are in condition of uncertainty, considering
the `fixed ones' as conditionands.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...hypergeometric.35
- Some care is needed
with this distribution because, as it is easy
to understand, different sets of parameters can be used.
For example, the app already
suggested [1] uses
with 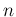 the sample size,
the sample size, 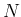 the population size and
the population size and
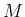 the number of white balls, thus leading to the
following correspondence with respect to the parameters
of the probability functions of the R language, to which
we are going to adhere in the text
the number of white balls, thus leading to the
following correspondence with respect to the parameters
of the probability functions of the R language, to which
we are going to adhere in the text
Expected value and variance are, using the app convention,
(In Wikipedia [4] there is a similar convention,
apart from the names, being the `random variable'
indicated by 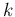 and the number of `white balls in the urn'
by
and the number of `white balls in the urn'
by 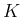 .)
.)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Carlo.36
- The R code
for
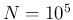 ,
, 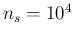 and
and 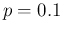 is provided in
Appendix B.3.
is provided in
Appendix B.3.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
infectees37
- We remind once more that this paper is rather
general, although motivated by Covid-19 related issues, and therefore
we also analyze the possibility of very large
 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... neglected.38
- Indeed, in such a limit
the condition (
![[*]](crossref.png) ) becomes
) becomes
whose solution is trivial, differing from
Eq. (![[*]](crossref.png) ) just
for the term at the denominator containing the factor
) just
for the term at the denominator containing the factor 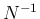 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....39
- This can be done evaluating
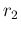 and
and 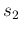 from
Eqs. (
from
Eqs. (![[*]](crossref.png) ) and (
) and (![[*]](crossref.png) )
with
)
with 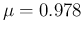 and
and
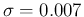 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...BUGS,40
-
Introducing MCMC and related algorithms
goes well beyond the purpose of this paper
and we recommend Ref. [5].
Moreover, mentioning the Gibbs Sampler algorithm applied to
probabilistic inference (and forecasting) it is impossible
not to refer to the BUGS project [6],
whose acronym stands
for Bayesian inference using
Gibbs Sampler, that has
been a kind of revolution in Bayesian analysis,
decades ago limited to simple cases because of computational problems
(see also Sec. 1 of Ref.[24]).
In the project web site [7]
it is possible to find packages with excellent Graphical User Interface,
tutorials and many examples [8].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... `object'.41
- To the returned object is assigned the name
`chain' in the script of Appendix B.6.
In order to get information about the kind of object,
just issue the command `str(chain)'.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... reasons.42
- Deviations from linearity
are expected for
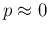 and rather small
and rather small 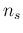 , but, as we have checked with approximated formulae,
the effect is negligible for the values of interest.
, but, as we have checked with approximated formulae,
the effect is negligible for the values of interest.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... B.8),43
- As alternative, one
could use JAGS, of which we provide the model
in Appendix B.9, leaving the R steering commands as exercise.
JAGS will be instead used in Sec.
![[*]](crossref.png) to infer
to infer 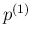 ,
,
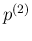 and
and
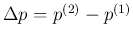 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... by44
- It might be useful to remind
that, given a linear combination
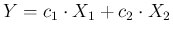 ,
the variance of
,
the variance of 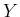 is given by
is given by
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... language.45
- The relation,
`
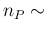 sum
sum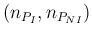 ' is
logically equivalent to
`
' is
logically equivalent to
`
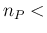 -
- 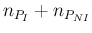 ', but
the latter instruction would not work
because JAGS prohibits `observed nodes'
to be defined by a deterministic assignment,
as, instead, it has been done in the case of
', but
the latter instruction would not work
because JAGS prohibits `observed nodes'
to be defined by a deterministic assignment,
as, instead, it has been done in the case of 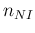 , defined
as `
, defined
as `
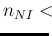 -
- 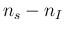 '.
'.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... case46
- Note that we can in principle
learn something
also about
 and
and  , because we can properly marginalize
Eq. (
, because we can properly marginalize
Eq. (![[*]](crossref.png) ) in order to get
) in order to get
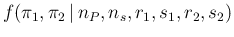 .
In the limit that they are very well known (condition
reflected
into very large
.
In the limit that they are very well known (condition
reflected
into very large 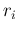 and
and 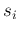 ) we expect that their joint probability
distribution is not updated much by the new pieces of information.
But, if instead they are poorly known, we get some information
on them, at the expense of the quality of information
we can get on the main quantity of interest, that is
) we expect that their joint probability
distribution is not updated much by the new pieces of information.
But, if instead they are poorly known, we get some information
on them, at the expense of the quality of information
we can get on the main quantity of interest, that is  (although we are not going into the
details, see Sec.
(although we are not going into the
details, see Sec. ![[*]](crossref.png) for a case in which
for a case in which
 is updated by the data).
is updated by the data).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... iterations.47
- Indeed
the traces show that the sampling is, so to say,
not optimal, and more iterations would be needed.
But for our needs here and for reminding the care
needed in applying this powerful tool,
we prefer to show this not ideal case of
sampling with a quite larger but not large enough
number of iterations. (Later on, when critical, we shall increase
nr up to
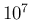 .)
.)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...#tex2html_wrap_inline12370#�48
- Plot and correlation coefficient
are obtained by the following R commands
chain.df <- as.data.frame( as.mcmc(chain) )
plot(chain.df, col='blue')
cor(chain.df)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... specificity.49
- In order
to avoid to modify the JAGS model, we simply multiply
all relevant Beta parameters by the large factor
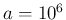 , thus reducing all uncertainties by a factor thousand
(see Eq. (
, thus reducing all uncertainties by a factor thousand
(see Eq. (![[*]](crossref.png) )).
This is done by adding the following command
)).
This is done by adding the following command
a=1e6; r1=r1*a; s1=s1*a; r2=r2*a; s2=s2*a
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....50
- We exploit
the same trick of the previous item redefining the Beta parameters
as follows
a=(22/7)^2; r2=r2*a; s2=s2*a
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
impossible.51
- In particular, we would like to point
out that this question has nothing to do with the story
of the `biased estimators' of frequentists. In probabilistic
inference the result is not just
a single number (the famous `estimator'), but rather
the distribution of the quantity of interest, of which
mean and standard deviation are only some of the possible
summaries, certainly the most convenient for several purposes.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
fail.52
- Although we cannot go through the details
in this paper, it would be interesting to
use `wider priors' about
 and
and  in order to see how they get updated by JAGS, and then
try to understand
what is going on making pairwise scatter plots of
the resulting
in order to see how they get updated by JAGS, and then
try to understand
what is going on making pairwise scatter plots of
the resulting  ,
,  and
and  .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....53
- It is worth pointing out
the cases, occurring especially in frontier science,
in which the likelihood is constant in some regions, and
therefore it does not update/reshape
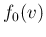 , where
`
, where
`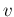 ' stands for the generic variable of interest
(see chapter 13 of Ref. [3]).
An interesting instance,
in which
' stands for the generic variable of interest
(see chapter 13 of Ref. [3]).
An interesting instance,
in which 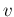 has the role of rate of gravitational
waves
has the role of rate of gravitational
waves 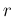 , is discussed in Ref. [10], where
the concept of relative belief updating ratio was first
introduced. Another frontier physics case, applied to the
Higgs boson mass
, is discussed in Ref. [10], where
the concept of relative belief updating ratio was first
introduced. Another frontier physics case, applied to the
Higgs boson mass 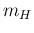 ,
on the basis of the experimental and theoretical information available
before year 1999, is reported in Ref. [11].
The two cases are complementary because in the first one
sensitivity is lost for
,
on the basis of the experimental and theoretical information available
before year 1999, is reported in Ref. [11].
The two cases are complementary because in the first one
sensitivity is lost for
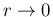 (`likelihood open
on the left side'), while in the
second for
(`likelihood open
on the left side'), while in the
second for
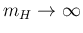 (`likelihood open on the right side').
(For recent developments and applications, see
Ref. [12].)
(`likelihood open on the right side').
(For recent developments and applications, see
Ref. [12].)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... step.54
- As
already remarked in footnote
![[*]](crossref.png) , `prior' does not
mean that you have to declare `before' you sit down to
make the inference! It just means that it is based on other
pieces of information (`knowledge')
on the quantity under study.
, `prior' does not
mean that you have to declare `before' you sit down to
make the inference! It just means that it is based on other
pieces of information (`knowledge')
on the quantity under study.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... deviation55
- See e.g. Sec. 2 of Ref. [13].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... priors.56
- The main reason of
the not excellent level of agreement
is due to the quite pronounced tail on the left
side of the distribution. The rule could work better
for other values of
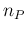 , given
, given 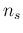 , but we have no interest
in showing the best case and try to sell it as `typical'.
We just stuck to the numeric case we have used mostly throughout
the paper.
, but we have no interest
in showing the best case and try to sell it as `typical'.
We just stuck to the numeric case we have used mostly throughout
the paper.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...fig:jags_inf_p_pi1_pi2.57
- The R package
PearsonDS [14] also contains
a random number generator, used in the script,
very convenient if further Monte Carlo integrations/simulations
starting from
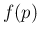 are needed.
are needed.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... imaginable.58
- It seems
(the episode has be referred to one of us
by a statistician present at the lectures) that in the 80's
Dennis Lindley ended a lecture series telling something like
“You see, I have shown you
a wonderful, logically consistent theory.
There is only a `little' problem.
We are unable to do the calculations
for the high dimensional problems that occur in real applications.”
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....59
- Remember that all elicitations of probabilities
always depend on some conditions/hypotheses/assumptions.
Therefore Eq. (A.2) should be written, more properly,
as
with 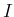 the (common!) background status of information under
which all probabilities appearing in the equation are evaluated,
although it is usually implicit in the equations to make them more
compact, as we have done in this paper.
the (common!) background status of information under
which all probabilities appearing in the equation are evaluated,
although it is usually implicit in the equations to make them more
compact, as we have done in this paper.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... connections60
- Causality
is notoriously something tricky,
and conditioning does not necessarily imply causation!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
![[*]](crossref.png) , although complemented by a rather popular
visualization of the question. But we have been surprised
by the lack of
any reference to probability theory and to the Bayes' rule
in the paper.
, although complemented by a rather popular
visualization of the question. But we have been surprised
by the lack of
any reference to probability theory and to the Bayes' rule
in the paper.
![[*]](crossref.png) )
- of no practical relevance, as we have already commented -
for
)
- of no practical relevance, as we have already commented -
for
![[*]](crossref.png) )
and (
)
and (![[*]](crossref.png) ) become then
) become then
![[*]](crossref.png) .)
.)
![[*]](crossref.png) ) derives from
) derives from
![[*]](crossref.png) (the one in which
(the one in which ![[*]](crossref.png) about the practical importance of using a flat prior,
because it is possible to modify the result
in a second step, `reshaping' the posterior
by personal, informative priors based on the best
knowledge of the problem, which might be different
for different experts (remember that the `prior'
does not imply time order, as remarked in
footnote
about the practical importance of using a flat prior,
because it is possible to modify the result
in a second step, `reshaping' the posterior
by personal, informative priors based on the best
knowledge of the problem, which might be different
for different experts (remember that the `prior'
does not imply time order, as remarked in
footnote ![[*]](crossref.png) ).
).
![[*]](crossref.png) for advice about the usage of mathematically convenient models.
for advice about the usage of mathematically convenient models.
![[*]](crossref.png) .
.
![[*]](crossref.png) we do not like to show a prior not vanishing at 1.
we do not like to show a prior not vanishing at 1.
![[*]](crossref.png) )
and even critical about the literal use of mathematical
expressions that should instead only be employed for convenience and
cum grano salis (see Sec.
)
and even critical about the literal use of mathematical
expressions that should instead only be employed for convenience and
cum grano salis (see Sec. ![[*]](crossref.png) ).
).![[*]](crossref.png) .)
.)
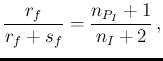
![[*]](crossref.png) ) and remembering that
) and remembering that
![[*]](crossref.png) ) can be approximated
as
) can be approximated
as
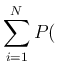 Inf
Inf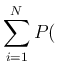 Inf
Inf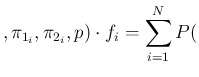 Inf
Inf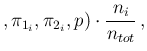
![[*]](crossref.png) )-(
)-(![[*]](crossref.png) ).
).![[*]](crossref.png) on the possible dependency of
on the possible dependency of ![[*]](crossref.png) showing
showing
![[*]](crossref.png) ) come from
Eq. (
) come from
Eq. (![[*]](crossref.png) ), in which the precise values
), in which the precise values
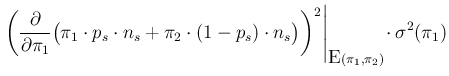
![[*]](crossref.png) we would get 0.194.
we would get 0.194.
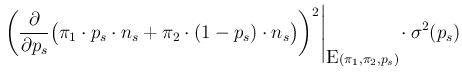
![[*]](crossref.png) ) becomes
) becomes
![\begin{displaymath}\begin{split}
\big[\mbox{E}(\pi_1)\cdot (1-\mbox{E}(\pi_1))\c...
..._1) \cdot p^2+\sigma^2(\pi_2)
\cdot (1-p)^2\big]\,,
\end{split}\end{displaymath}](img560.png)
![[*]](crossref.png) ) just
for the term at the denominator containing the factor
) just
for the term at the denominator containing the factor ![[*]](crossref.png) ) and (
) and (![[*]](crossref.png) )
with
)
with ![[*]](crossref.png) to infer
to infer ![[*]](crossref.png) ) in order to get
) in order to get
![[*]](crossref.png) for a case in which
for a case in which
![[*]](crossref.png) )).
This is done by adding the following command
)).
This is done by adding the following command
![[*]](crossref.png) , `prior' does not
mean that you have to declare `before' you sit down to
make the inference! It just means that it is based on other
pieces of information (`knowledge')
on the quantity under study.
, `prior' does not
mean that you have to declare `before' you sit down to
make the inference! It just means that it is based on other
pieces of information (`knowledge')
on the quantity under study.