As we have already well understood, the uncertainty
on the result is highly dependent of the
uncertainty concerning  and
and  .
Therefore, as we have done in the previous sections,
let us also change here our
assumptions and see how the main result changes
accordingly (
.
Therefore, as we have done in the previous sections,
let us also change here our
assumptions and see how the main result changes
accordingly (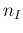 is of little interest, at this point,
also because of its very high correlation with
is of little interest, at this point,
also because of its very high correlation with  ,
and hence we shall not monitor it any longer in further examples).
,
and hence we shall not monitor it any longer in further examples).
- First we start assuming negligible uncertainty
on sensitivity and specificity.49 As a result, the standard
uncertainty
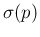 becomes
becomes 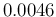 ,
that is about a factor
,
that is about a factor 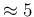 smaller.
smaller.
- Then, as we have done in the above sections,
we keep
 to its default value (
to its default value (
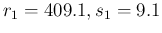 ),
only reducing the uncertainty of
),
only reducing the uncertainty of  to
to 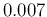 .50 Also in this case the uncertainty decreases,
getting
.50 Also in this case the uncertainty decreases,
getting
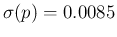 .
.
- Finally, we make the pdf of
 mirror symmetric
with respect to that of
mirror symmetric
with respect to that of  , that is
, that is
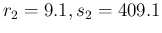 .
But, obviously we need to change the number of the
observed positives, choosing this time 1170,
as suggested by our expectations
(see Fig.
.
But, obviously we need to change the number of the
observed positives, choosing this time 1170,
as suggested by our expectations
(see Fig. ![[*]](crossref.png) ).
As a result we get
).
As a result we get
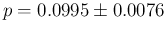 , with an uncertainty
not differing so much with respect to the previous case.
Indeed, as we have
have already noted in the previous sections,
improving the specificity (
, with an uncertainty
not differing so much with respect to the previous case.
Indeed, as we have
have already noted in the previous sections,
improving the specificity ( reduced by a factor five)
has only a little effect on the quality of the measurement,
being more important the uncertainty with which
that test parameter is known. (And we expect that something like that
is also true for the sensitivity.)
reduced by a factor five)
has only a little effect on the quality of the measurement,
being more important the uncertainty with which
that test parameter is known. (And we expect that something like that
is also true for the sensitivity.)
![[*]](crossref.png) ).
As a result we get
).
As a result we get