A more systematic study of the quality of the inference is shown
in Tab. ![[*]](crossref.png) ,
,
Table:
Proportion  of infected in a population, inferred from
the number
of infected in a population, inferred from
the number 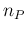 of positives in a sample of
of positives in a sample of 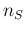 individuals. The three blocks
of the table corresponds to the assumptions summarized by
individuals. The three blocks
of the table corresponds to the assumptions summarized by
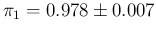 and
and
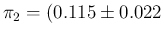 ,
,
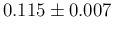 ,
,
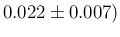 .
.
|
|
which reports the
inferred value of  , summarized by the expected value and its standard
deviation evaluated by sampling, as a function
of the sample size and the number of positives in the sample.
The three blocks of the
table correspond to our typical hypotheses on the knowledge of
sensitivity and specificity, and summarized, from top to bottom,
by
, summarized by the expected value and its standard
deviation evaluated by sampling, as a function
of the sample size and the number of positives in the sample.
The three blocks of the
table correspond to our typical hypotheses on the knowledge of
sensitivity and specificity, and summarized, from top to bottom,
by
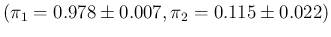 ,
,
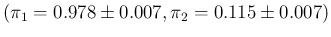 and
and
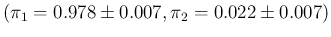 ,
corresponding then to the cases shown, in the same order, in
Figs.
,
corresponding then to the cases shown, in the same order, in
Figs. ![[*]](crossref.png) -
-![[*]](crossref.png) (we have added an extra column with the numbers of
positives yielding
(we have added an extra column with the numbers of
positives yielding
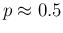 ).
We see that, from columns 2 to 6, we get
).
We see that, from columns 2 to 6, we get
 ranging from
ranging from 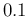 to
to 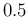 at steps of
at steps of 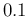 , with
standard uncertainty varying with
, with
standard uncertainty varying with 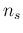 and
and 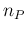 (and therefore with
the fraction of positives
(and therefore with
the fraction of positives 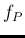 ) in agreement with what
we have learned in Sec.
) in agreement with what
we have learned in Sec. ![[*]](crossref.png) , studying the
predictive distributions (note the difference between resolution
power, used there, and standard uncertainty, used here).
, studying the
predictive distributions (note the difference between resolution
power, used there, and standard uncertainty, used here).
We note that, instead, the results of the first column is
“not around zero, as expected” (naively).
The reason is very simple and it is illustrated in
Fig. ![[*]](crossref.png) for the case of
for the case of 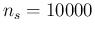 .
.
Figure:
Inference of  from
from 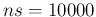 and
and 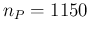 .
.
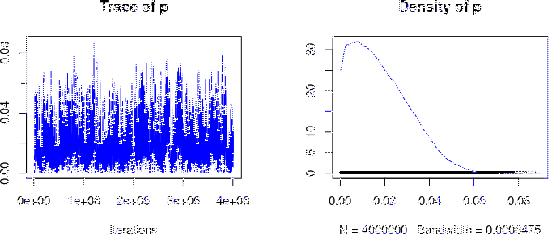 |
It is true that, if there were no infected in the population,
then we would expect
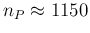 (with a standard uncertainty of 220),
but the distribution of
(with a standard uncertainty of 220),
but the distribution of  provided by the inference cannot have
a mean value zero, simply because negative values of
provided by the inference cannot have
a mean value zero, simply because negative values of  are
impossible.51Obviously the smaller is the number of positives in the sample
and more peaked is the distribution of
are
impossible.51Obviously the smaller is the number of positives in the sample
and more peaked is the distribution of  close to 0. But what happens
if, for
close to 0. But what happens
if, for 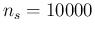 ,
, 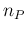 is much smaller of 1150?
This interesting case will be the subject of the next subsection.
is much smaller of 1150?
This interesting case will be the subject of the next subsection.
![[*]](crossref.png) ,
,
![[*]](crossref.png) -
-![[*]](crossref.png) (we have added an extra column with the numbers of
positives yielding
(we have added an extra column with the numbers of
positives yielding
![[*]](crossref.png) , studying the
predictive distributions (note the difference between resolution
power, used there, and standard uncertainty, used here).
, studying the
predictive distributions (note the difference between resolution
power, used there, and standard uncertainty, used here).
![[*]](crossref.png) for the case of
for the case of ![]() .
.