Updated knowledge of
 and
and  in the case of
`anomalous' number of positives
in the case of
`anomalous' number of positives
Let us imagine that, instead of 1150 positives, we `had observed'
a much smaller number (in terms of standard deviation of prediction,
that, we remind, is about 220). For example, an under-fluctuation
of 3 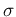 's would yield 490 positives. But let us exaggerate
and take as few as 50 positives, corresponding to
's would yield 490 positives. But let us exaggerate
and take as few as 50 positives, corresponding to
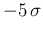 's.
The JAGS result (this time
monitoring also
's.
The JAGS result (this time
monitoring also  and
and  ),
obtained using our usual uncertainties concerning
),
obtained using our usual uncertainties concerning
 and
and  (
(
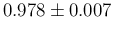 and
and
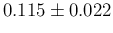 , respectively),
is showed in Fig.
, respectively),
is showed in Fig. ![[*]](crossref.png)
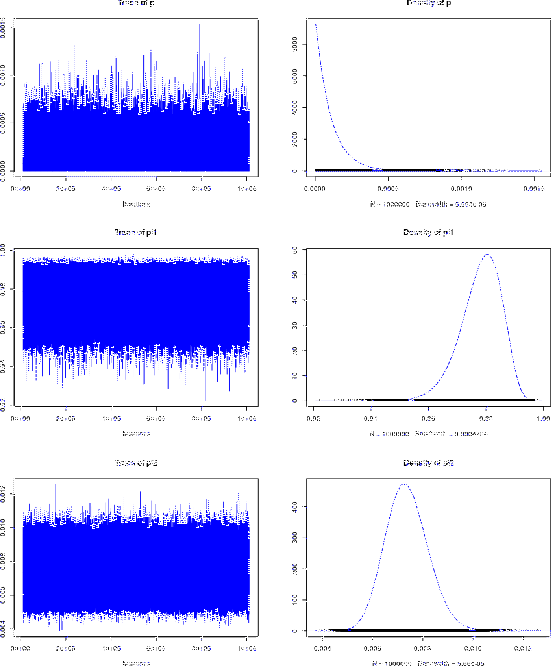
Figure:
JAGS inference of  ,
,  and
and  from
from 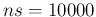 and
and 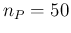 (see text).
(see text).
 |
and summarized as
1. Empirical mean and standard deviation for each variable,
plus standard error of the mean:
Mean SD Naive SE Time-series SE
p 0.0001022 0.0001023 1.023e-07 1.998e-07
pi1 0.9781819 0.0071445 7.145e-06 7.161e-06
pi2 0.0073581 0.0008463 8.463e-07 8.463e-07
2. Quantiles for each variable:
2.5% 25% 50% 75% 97.5%
p 2.586e-06 2.949e-05 7.091e-05 0.0001415 0.0003771
pi1 9.622e-01 9.738e-01 9.789e-01 0.9833334 0.9899013
pi2 5.790e-03 6.771e-03 7.327e-03 0.0079113 0.0091035
As we see, the distribution of  looks exponential,
with mean and standard deviation practically identical
and equal to
looks exponential,
with mean and standard deviation practically identical
and equal to
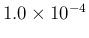 (we remind that it is
a property of the exponential distribution to have
expected value and standard deviation equal).
In this case the quantiles produced by
(we remind that it is
a property of the exponential distribution to have
expected value and standard deviation equal).
In this case the quantiles produced by 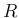 are particularly
interesting, providing e.g.
are particularly
interesting, providing e.g.
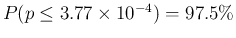 .
.
The fact that a small number of infectees squeezes the distribution of  towards zero follows the expectations. More surprising, at first sight,
is the fact that also the value of
towards zero follows the expectations. More surprising, at first sight,
is the fact that also the value of  does change:
does change:
The reason why  can change
(also
can change
(also  could, although JAGS `thinks' this is not the case)
is due to the fact that it is now a unobserved node,
and the
Beta
could, although JAGS `thinks' this is not the case)
is due to the fact that it is now a unobserved node,
and the
Beta with
which we model it is just the prior distribution we assign to it.
In other words,
the very small number of positives could be not only due to a very small value
of
with
which we model it is just the prior distribution we assign to it.
In other words,
the very small number of positives could be not only due to a very small value
of  , but also to the possibility that
, but also to the possibility that  is indeed
substantially smaller than what we
initially thought. This sounds absolutely reasonable,
but telling exactly what the result will
be can only be done using strictly the rules of
probability theory,
although with the help of MCMC, because
in multivariate problems of this kind intuition can easily
fail.52
is indeed
substantially smaller than what we
initially thought. This sounds absolutely reasonable,
but telling exactly what the result will
be can only be done using strictly the rules of
probability theory,
although with the help of MCMC, because
in multivariate problems of this kind intuition can easily
fail.52
![[*]](crossref.png) and summarized as
and summarized as
![]() towards zero follows the expectations. More surprising, at first sight,
is the fact that also the value of
towards zero follows the expectations. More surprising, at first sight,
is the fact that also the value of ![]() does change:
does change: