In Sec. ![[*]](crossref.png) we have considered
the numbers of positives and negatives that we
expect to observe, analyzing 10000 individuals,
using our initial parameters
(
we have considered
the numbers of positives and negatives that we
expect to observe, analyzing 10000 individuals,
using our initial parameters
(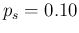 ,
,
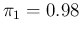 ,
,
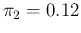 ) but
without taking into account the unavoidable
`statistical fluctuation'. We do it now, using the
probabilistic graphical model shown
in Fig.
) but
without taking into account the unavoidable
`statistical fluctuation'. We do it now, using the
probabilistic graphical model shown
in Fig. ![[*]](crossref.png) ,
,
Figure:
Graphical model in which the number of positives
could come from infected or not infected individuals. Arrows with
dashed lines stand for a deterministic link, being
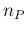 simply equal to the sum of
simply equal to the sum of 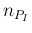 and
and
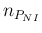 .
.
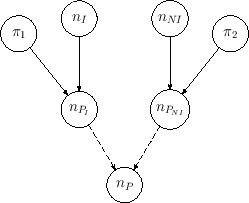 |
obtained by doubling the basic one
of Fig. ![[*]](crossref.png) , one branch
for the infectees and a second for the others. Then the numbers
of positives resulting from the two contributions are added up.
Note in Fig.
, one branch
for the infectees and a second for the others. Then the numbers
of positives resulting from the two contributions are added up.
Note in Fig. ![[*]](crossref.png) the dashed arrows from the nodes
the dashed arrows from the nodes 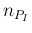 and
and
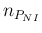 to the node
to the node 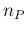 :
they indicate a deterministic link,28being
:
they indicate a deterministic link,28being
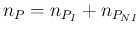 .
.
The probability distribution of 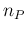 is with good approximation
Gaussian, due to the well known large numbers behavior of the
binomial distribution (and, moreover,
to the properties of the sum of `random variables').
On the other hand, the expected value and the standard deviation of
is with good approximation
Gaussian, due to the well known large numbers behavior of the
binomial distribution (and, moreover,
to the properties of the sum of `random variables').
On the other hand, the expected value and the standard deviation of 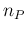 can been
calculated exactly, using the properties
of expected values and variances, thus getting
(summarizing for sake of space with the
symbol
can been
calculated exactly, using the properties
of expected values and variances, thus getting
(summarizing for sake of space with the
symbol 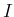 , staying for all available information,
the conditions on which the
various quantities depend):
, staying for all available information,
the conditions on which the
various quantities depend):
with 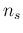 the sample size.
Expected value and standard deviation
of the fraction of the number of individuals
tagged as positive (
the sample size.
Expected value and standard deviation
of the fraction of the number of individuals
tagged as positive (
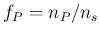 ) are then
) are then
For example, making use of our reference numbers
(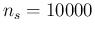 ,
,
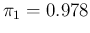 and
and
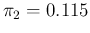 )
we get for some
values of
)
we get for some
values of  (expected value
(expected value 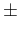 standard uncertainty):
standard uncertainty):
From this numbers we can get an idea about the precision
we could get on  , if
, if  and
and  were
perfectly known, although their values are rather far from
what one would ideally desire. For example, since under the hypotheses
were
perfectly known, although their values are rather far from
what one would ideally desire. For example, since under the hypotheses
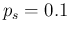 and
and 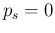 (and similar numbers are obtained
varying
(and similar numbers are obtained
varying  from
from 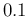 to
to 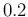 ) the expected difference of
positives is
) the expected difference of
positives is
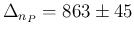 , it follows that,
varying
, it follows that,
varying  by
by 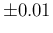 the expected number of positives would vary
by
the expected number of positives would vary
by
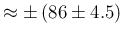 . This means that, roughly speaking,
it could be possible to estimate
. This means that, roughly speaking,
it could be possible to estimate  with an uncertainty
of
with an uncertainty
of 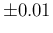 or better.
or better.
Before taking into account the effects due to the uncertainties
of  and
and  , let us
also see how the quality of the measurement depends on the sample size.
In order to do this, we fix this time
, let us
also see how the quality of the measurement depends on the sample size.
In order to do this, we fix this time  to our arbitrary value of
to our arbitrary value of 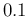 and vary the sample size by about half order of
magnitude (that is
and vary the sample size by about half order of
magnitude (that is
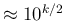 , with
, with
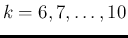 ),
reporting in this case directly the expected
fraction of positives:
),
reporting in this case directly the expected
fraction of positives:
As we can see, if we knew perfectly  and
and  ,
already a sample of a few thousands individuals would allow us to
predict the fraction of tagged positives with a relative
uncertainty of a few percent.
However there are other effects to be taken into account:
,
already a sample of a few thousands individuals would allow us to
predict the fraction of tagged positives with a relative
uncertainty of a few percent.
However there are other effects to be taken into account:
- there is uncertainty about
 and
and  ;
;
- the proportion of infectees in the
sample is different from that in the population
(that is, in general
 differs from
differs from  );
);
- the inference from the observed numbers of positives to
 , and then to
, and then to  , has to be done using
sound probabilistic inferential methods.
, has to be done using
sound probabilistic inferential methods.
![[*]](crossref.png) we have considered
the numbers of positives and negatives that we
expect to observe, analyzing 10000 individuals,
using our initial parameters
(
we have considered
the numbers of positives and negatives that we
expect to observe, analyzing 10000 individuals,
using our initial parameters
(![[*]](crossref.png) ,
,

![[*]](crossref.png) , one branch
for the infectees and a second for the others. Then the numbers
of positives resulting from the two contributions are added up.
Note in Fig.
, one branch
for the infectees and a second for the others. Then the numbers
of positives resulting from the two contributions are added up.
Note in Fig. ![[*]](crossref.png) the dashed arrows from the nodes
the dashed arrows from the nodes ![]() is with good approximation
Gaussian, due to the well known large numbers behavior of the
binomial distribution (and, moreover,
to the properties of the sum of `random variables').
On the other hand, the expected value and the standard deviation of
is with good approximation
Gaussian, due to the well known large numbers behavior of the
binomial distribution (and, moreover,
to the properties of the sum of `random variables').
On the other hand, the expected value and the standard deviation of ![]() can been
calculated exactly, using the properties
of expected values and variances, thus getting
(summarizing for sake of space with the
symbol
can been
calculated exactly, using the properties
of expected values and variances, thus getting
(summarizing for sake of space with the
symbol ![]() , staying for all available information,
the conditions on which the
various quantities depend):
, staying for all available information,
the conditions on which the
various quantities depend):
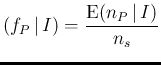
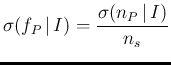
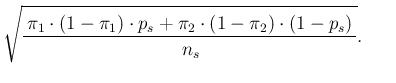
![]() and
and ![]() , let us
also see how the quality of the measurement depends on the sample size.
In order to do this, we fix this time
, let us
also see how the quality of the measurement depends on the sample size.
In order to do this, we fix this time ![]() to our arbitrary value of
to our arbitrary value of ![]() and vary the sample size by about half order of
magnitude (that is
and vary the sample size by about half order of
magnitude (that is
![]() , with
, with
![]() ),
reporting in this case directly the expected
fraction of positives:
),
reporting in this case directly the expected
fraction of positives: