It is rather obvious to think that, repeating the same test with
samples of exactly the same size, but involving
different individuals, no one would be surprised
to count different numbers of positives and negatives in the two samples.
In fact, sticking for a while only to infectees and
assuming an exact value of  , the number
, the number 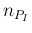 of positives
is given by the binomial distribution,
of positives
is given by the binomial distribution,
that is, in short (with `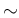 ' to be read as `follows...'),
' to be read as `follows...'),
The probability distribution (![[*]](crossref.png) ) describes
how much we have to rationally believe to observe
the possible values of
) describes
how much we have to rationally believe to observe
the possible values of 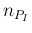 (integers between 0 and
(integers between 0 and 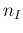 ),
given
),
given 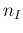 and
and  .
.
An inverse problem is to infer
 , given
, given 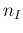 and the observed number
and the observed number 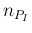 (indeed, there is also a second inverse problem, that is inferring
(indeed, there is also a second inverse problem, that is inferring
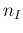 from
from 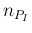 and
and  - the three problems
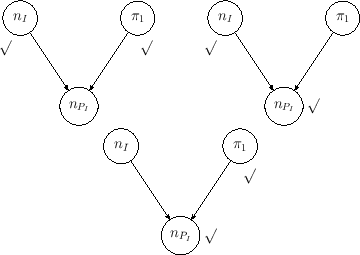
are represented graphically by the networks
of Fig.
- the three problems
are represented graphically by the networks
of Fig. ![[*]](crossref.png) ).
).
Figure:
Graphical models of the binomial
distribution (left) and its `inverse problems'. The symbol
` ' indicates the `observed' nodes
of the network, that is the value of the quantity
associated to it
is (assumed to be) certain. The other node
(only one in this simple case)
is `unobserved' and it is associated to
a quantity whose value is uncertain.
' indicates the `observed' nodes
of the network, that is the value of the quantity
associated to it
is (assumed to be) certain. The other node
(only one in this simple case)
is `unobserved' and it is associated to
a quantity whose value is uncertain.
 |
This is the kind of
Problem in the Doctrine of Chances first solved by
Bayes [35],
and, independently and in a more refined way, by
Laplace [27] about 250 years ago.
Applying the result of probability theory that
nowadays goes under the name of
Bayes' theorem (or Bayes' rule) that we
have introduced in the previous section, we get, apart from the
normalization factor
 hereafter the same generic
symbol is
used for both probability functions and
probability density functions (pdf), being the meaning clear from the
context
hereafter the same generic
symbol is
used for both probability functions and
probability density functions (pdf), being the meaning clear from the
context![$]$](img65.png) :15
:15
where
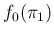 is the prior pdf, that describes how we believe
in the possible values of
is the prior pdf, that describes how we believe
in the possible values of  `before' (see
footnote
`before' (see
footnote ![[*]](crossref.png) and Sec.
and Sec. ![[*]](crossref.png) )
we get the knowledge
of the experiment
resulting into
)
we get the knowledge
of the experiment
resulting into 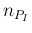 successes in
successes in 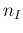 trials.
Naively one could say that all possible values of
trials.
Naively one could say that all possible values of  are equally possible, thus resulting in
are equally possible, thus resulting in
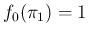 .
But this is absolutely unreasonable,16in the case of instrumentation
and procedures devised by experts in order
to hopefully tag infected people as positive.
Therefore the value of
.
But this is absolutely unreasonable,16in the case of instrumentation
and procedures devised by experts in order
to hopefully tag infected people as positive.
Therefore the value of  should be most likely
in the region above
should be most likely
in the region above
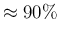 , though without sharp cut below it.
Similarly, reasonable values of
, though without sharp cut below it.
Similarly, reasonable values of  are expected
to be in the region below
are expected
to be in the region below
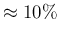 .
.
![[*]](crossref.png) ) describes
how much we have to rationally believe to observe
the possible values of
) describes
how much we have to rationally believe to observe
the possible values of ![]() , given
, given ![]() and the observed number
and the observed number ![]() (indeed, there is also a second inverse problem, that is inferring
(indeed, there is also a second inverse problem, that is inferring
![]() from
from ![]() and
and ![]() - the three problems
are represented graphically by the networks
of Fig.
- the three problems
are represented graphically by the networks
of Fig. ![[*]](crossref.png) ).
).

![[*]](crossref.png) and Sec.
and Sec. ![[*]](crossref.png) )
we get the knowledge
of the experiment
resulting into
)
we get the knowledge
of the experiment
resulting into