Conjugate priors
At this point, remembering Laplace's dictum that
“probability is good sense reduced to a calculus”,
we need to model the prior in a reasonable but mathematically
convenient way.17A good compromise for this kind of problem
is the Beta probability
function, which we remind here, written
for the generic variable 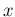 and neglecting
multiplicative factors in order to focus, at this point,
on its structure:18
and neglecting
multiplicative factors in order to focus, at this point,
on its structure:18
We see that for 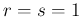 a uniform distribution is recovered.
An important remark is that for
a uniform distribution is recovered.
An important remark is that for 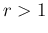 the pdf vanishes
at
the pdf vanishes
at 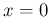 ; for
; for 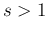 it vanishes at
it vanishes at 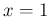 . It follows
that,
if
. It follows
that,
if 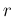 and
and 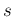 are both above 1, we can see at a glance
that the function has a single maximum.
It is easy to calculate that it occurs at (`modal value')
are both above 1, we can see at a glance
that the function has a single maximum.
It is easy to calculate that it occurs at (`modal value')
Expected value and variance
(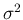 ) are
) are
In the case of uniform distribution, recovered by 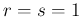 , we obtain the well known
E
, we obtain the well known
E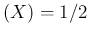 and
and
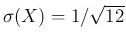 (and, obviously, there is no
single modal value).
For large
(and, obviously, there is no
single modal value).
For large 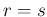 , we get
, we get
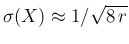 : as the values
of
: as the values
of 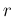 and
and 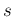 increases, the
distribution becomes very narrow around
increases, the
distribution becomes very narrow around 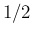 .
.
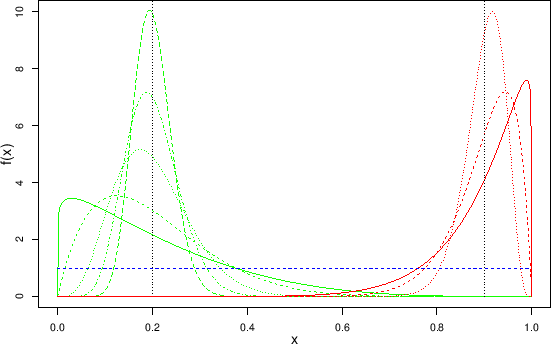
Figure:
Examples of Beta distributions.
The curves preferring small values of the generic variable 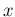 ,
all having
E
,
all having
E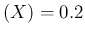 are obtained with (widest to narrowest)
are obtained with (widest to narrowest)
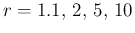 and
and 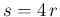 (
( : 0.16, 0.12, 0.078, 0.056).
Those preferring larger
values of
: 0.16, 0.12, 0.078, 0.056).
Those preferring larger
values of 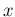 ,
all having
E
,
all having
E are obtained with (again widest to narrowest)
are obtained with (again widest to narrowest)
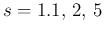 and
and 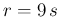 (
(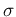 : 0.087, 0.065, 0.042).
: 0.087, 0.065, 0.042).
 |
Examples, with values of 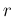 and
and 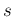 to possibly model
the priors we are interested in,
are shown in Fig.
to possibly model
the priors we are interested in,
are shown in Fig. ![[*]](crossref.png) .
.
Using the Beta distribution for
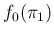 , our inferential problem
is promptly solved, since
Eq. (
, our inferential problem
is promptly solved, since
Eq. (![[*]](crossref.png) )
becomes, besides a normalization factor and with parameters indicated
as
)
becomes, besides a normalization factor and with parameters indicated
as 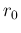 and
and 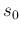 in order to remind their role of prior parameters,
in order to remind their role of prior parameters,
So, the posterior is still a Beta distribution, with parameters
updated according to the simple rules
For this
reason the Beta is known to be the prior conjugate
of the binomial distribution. In terms of our variables,
The advantage of using the Beta prior conjugate
is self-evident, if we can choose values of 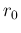 and
and 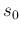 that reasonably
model our prior belief about
that reasonably
model our prior belief about  . For this
reason it might be useful to invert Eq. (
. For this
reason it might be useful to invert Eq. (![[*]](crossref.png) )
and (
)
and (![[*]](crossref.png) ), thus getting
), thus getting
So, for example, if we think that  should be
around 0.95 with a standard uncertainty of about
should be
around 0.95 with a standard uncertainty of about 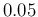 ,
we get then
,
we get then
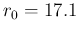 and
and 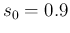 , the latter
slightly increased `by hand' to
, the latter
slightly increased `by hand' to
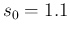 because our rational
prior has to assign zero probability to
because our rational
prior has to assign zero probability to 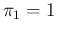 ,
that would imply the possibility of
a perfect test.19The experimental data update then
,
that would imply the possibility of
a perfect test.19The experimental data update then
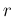 and
and 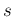 to
to
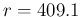 and
and
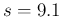 .
For
.
For  we model a symmetric prior, with expected value 0.05
and
we model a symmetric prior, with expected value 0.05
and
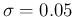 . We just need to swap
. We just need to swap 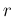 and
and 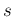 , thus getting
, thus getting
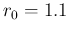 and
and 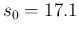 , updated by the data
to
, updated by the data
to
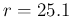 and
and
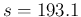 . The results
are shown in Fig.
. The results
are shown in Fig. ![[*]](crossref.png) .
.
Figure:
Priors (dashed) and posterior (solid)
probability density functions
of  and
and  .
.
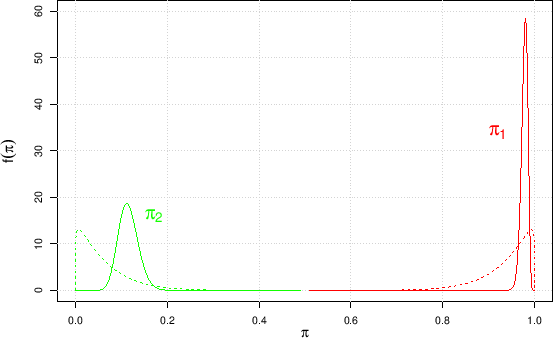 |
Expressed in terms of
expected value 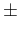 standard deviation they are
standard deviation they are
As we can easily guess, using simply 0.98 and 0.12, as we have
done in the previous sections, will give essentially the same results,
in terms of expectations. Anyway, in order to be internally consistent
hereafter our reference values
will be
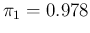 and
and
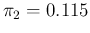 .20
.20
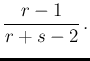

![[*]](crossref.png) .
.
![]() , our inferential problem
is promptly solved, since
Eq. (
, our inferential problem
is promptly solved, since
Eq. (![[*]](crossref.png) )
becomes, besides a normalization factor and with parameters indicated
as
)
becomes, besides a normalization factor and with parameters indicated
as ![]() and
and ![]() in order to remind their role of prior parameters,
in order to remind their role of prior parameters,
![[*]](crossref.png) )
and (
)
and (![[*]](crossref.png) ), thus getting
), thus getting
![[*]](crossref.png) .
Expressed in terms of
expected value
.
Expressed in terms of
expected value