At this point someone would object that one should use
the most probable values of  and
and  , rather than their
expected values. The answer is rather simple.
Let us consider again Eq. (
, rather than their
expected values. The answer is rather simple.
Let us consider again Eq. (![[*]](crossref.png) ).
Assuming a well precise value of
).
Assuming a well precise value of  , the probability of Positive
if Infected is exactly equal to
, the probability of Positive
if Infected is exactly equal to  .
However, if we want to evaluate
.
However, if we want to evaluate
 Pos
Pos Inf
Inf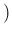 , taking into account all possible
values of
, taking into account all possible
values of  and how much we believe each of them,
that is
and how much we believe each of them,
that is 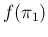 ,
we just to need to use a well known result of
probability theory:
,
we just to need to use a well known result of
probability theory:
But, being
 Pos
Pos Inf
Inf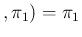 , we get
, we get
in which we recognize the expected value of
 .21
.21
![[*]](crossref.png) ).
Assuming a well precise value of
).
Assuming a well precise value of 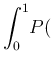 Pos
Pos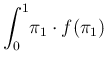 d
d