Effect of the
uncertainties on  and
and  on the probabilities
of interest
on the probabilities
of interest
The immediate question that follows is how the uncertainties
concerning these two parameters change the probabilities
of interest. We start reporting in Tab. ![[*]](crossref.png)
Table:
Probability of Infected and Not Infected, given the
test result, as a function of the model parameters.
The third and fourth rows, in boldface,
are for our reference values of  and
and  . The last
two rows are the results `integrating over' all the possibilities
of
. The last
two rows are the results `integrating over' all the possibilities
of  and
and  , according to
Eq. (
, according to
Eq. (![[*]](crossref.png) ) and
(
) and
(![[*]](crossref.png) ),
with the integrals done in practice by Monte Carlo sampling.
),
with the integrals done in practice by Monte Carlo sampling.
|
|
the dependence of
 Inf
Inf Pos
Pos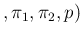 and
and
 NoInf
NoInf Neg
Neg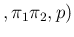 , on which we particularly
focused in the previous sections, on the three parameters.
The dependence on
, on which we particularly
focused in the previous sections, on the three parameters.
The dependence on  is shown in the different columns, while
the sets of
is shown in the different columns, while
the sets of  and
and  are written explicitly in the
conditionands of the different probabilities.
We start from the nominal values of 0.98 and 0.12 taken from
Ref. [16] (first two rows of the table).
Then we use the expected values calculated
in the previous section (third and fourth rows, in boldface), followed
by variations of
are written explicitly in the
conditionands of the different probabilities.
We start from the nominal values of 0.98 and 0.12 taken from
Ref. [16] (first two rows of the table).
Then we use the expected values calculated
in the previous section (third and fourth rows, in boldface), followed
by variations of  and
and  based on
based on
 one standard deviation
from their expected values.
one standard deviation
from their expected values.
We see that the probabilities
of interest do not change significantly, the main effect
being due to the assumed proportion of infectees in the
population. One could argue that the dependence on
 and
and  could be larger, if larger deviations
of the parameters were considered.
Obviously this is true, but one has to
take also into account the (small)
probabilities of large deviations
from the mean values, especially if we allow
simultaneous deviations of both parameters.
could be larger, if larger deviations
of the parameters were considered.
Obviously this is true, but one has to
take also into account the (small)
probabilities of large deviations
from the mean values, especially if we allow
simultaneous deviations of both parameters.
A more relevant question is, instead, how do
 Inf
Inf Pos
Pos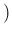 and
and
 NoInf
NoInf Neg) change, if we take into
account all possible variations of the two parameters
(weighed by their probabilities!).
This is easily done, applying the result of
probability theory that we have already used above.
We get, for the probabilities we are mostly interested in,
Neg) change, if we take into
account all possible variations of the two parameters
(weighed by their probabilities!).
This is easily done, applying the result of
probability theory that we have already used above.
We get, for the probabilities we are mostly interested in,
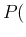 Inf Inf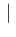 Pos Pos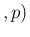 |
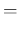 |
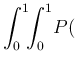 Inf Inf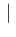 Pos Pos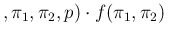 d d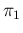 d d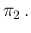 |
(39) |
| |
|
|
|
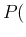 NoInf NoInf Neg Neg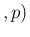 |
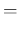 |
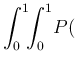 NoInf NoInf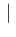 Neg Neg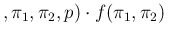 d d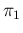 d d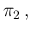 |
(40) |
where
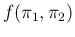 can be factorized into
can be factorized into
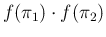 .22The integral can be easily done by Monte Carlo,23whose implementation in the R language [25], both for
.22The integral can be easily done by Monte Carlo,23whose implementation in the R language [25], both for
 Inf
Inf Pos
Pos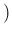 and
and
 NoInf
NoInf Neg
Neg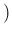 , is
given in Appendix B.1.
, is
given in Appendix B.1.
We get, for our arbitrary reference value of 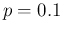 ,
,
 Inf
Inf Pos
Pos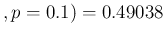 and
and
 NoInf
NoInf Neg
Neg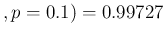 , to be compared
to 0.4858 and 0.9973, respectively, if the expected values were used.
The results, shown with an exaggerated number of digits
just to appreciate tiny differences, are practically the same.
This result could sound counter-intuitive, especially if
one thinks that
, to be compared
to 0.4858 and 0.9973, respectively, if the expected values were used.
The results, shown with an exaggerated number of digits
just to appreciate tiny differences, are practically the same.
This result could sound counter-intuitive, especially if
one thinks that  has an almost 20% intrinsic
standard uncertainty.
The reason is due to the fact that the dependence of the
probabilities of interest on
has an almost 20% intrinsic
standard uncertainty.
The reason is due to the fact that the dependence of the
probabilities of interest on  and
and  is rather linear in the region where their probability
mass is concentrated, as shown in Fig.
is rather linear in the region where their probability
mass is concentrated, as shown in Fig. ![[*]](crossref.png) .
.
Figure:
Dependence of
 Inf
Inf Pos
Pos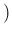 (upper plots) and
(upper plots) and
 NoInf
NoInf Neg
Neg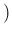 (lower plots)
on
(lower plots)
on  (left hand plots, for
(left hand plots, for
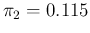 and
and 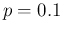 ) and on
) and on  (right hand plots, for
(right hand plots, for
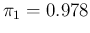 and
and 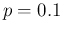 ). The parameters
). The parameters  and
and  are
allowed to change withing a range of
are
allowed to change withing a range of
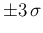 's around
their expected values.
's around
their expected values.
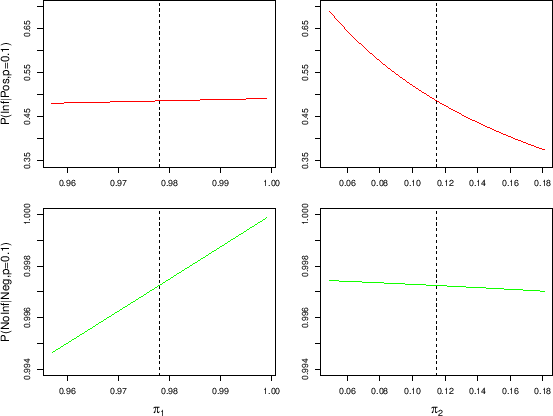 |
This rather good linearity causes a high degree of cancellations
in the integral.24This explains why the only perceptible effect appears
in
 Inf
Inf Pos
Pos , slightly
larger than the number calculated at the expected values
(49.04% vs 48.58%), caused by the small non-linearity
of that probability as a function of
, slightly
larger than the number calculated at the expected values
(49.04% vs 48.58%), caused by the small non-linearity
of that probability as a function of  ,
as shown in the upper, right hand plot of
Fig.
,
as shown in the upper, right hand plot of
Fig. ![[*]](crossref.png) : symmetric
variations of
: symmetric
variations of  cause slightly
asymmetric variations of
cause slightly
asymmetric variations of
 Inf
Inf Pos
Pos ,
thus slightly favoring higher
values of that probability.
,
thus slightly favoring higher
values of that probability.
![[*]](crossref.png)
![]() and
and ![]() could be larger, if larger deviations
of the parameters were considered.
Obviously this is true, but one has to
take also into account the (small)
probabilities of large deviations
from the mean values, especially if we allow
simultaneous deviations of both parameters.
could be larger, if larger deviations
of the parameters were considered.
Obviously this is true, but one has to
take also into account the (small)
probabilities of large deviations
from the mean values, especially if we allow
simultaneous deviations of both parameters.
![]() Inf
Inf![]() Pos
Pos![]() and
and
![]() NoInf
NoInf![]() Neg) change, if we take into
account all possible variations of the two parameters
(weighed by their probabilities!).
This is easily done, applying the result of
probability theory that we have already used above.
We get, for the probabilities we are mostly interested in,
Neg) change, if we take into
account all possible variations of the two parameters
(weighed by their probabilities!).
This is easily done, applying the result of
probability theory that we have already used above.
We get, for the probabilities we are mostly interested in,
![]() ,
,
![]() Inf
Inf![]() Pos
Pos![]() and
and
![]() NoInf
NoInf![]() Neg
Neg![]() , to be compared
to 0.4858 and 0.9973, respectively, if the expected values were used.
The results, shown with an exaggerated number of digits
just to appreciate tiny differences, are practically the same.
This result could sound counter-intuitive, especially if
one thinks that
, to be compared
to 0.4858 and 0.9973, respectively, if the expected values were used.
The results, shown with an exaggerated number of digits
just to appreciate tiny differences, are practically the same.
This result could sound counter-intuitive, especially if
one thinks that ![]() has an almost 20% intrinsic
standard uncertainty.
The reason is due to the fact that the dependence of the
probabilities of interest on
has an almost 20% intrinsic
standard uncertainty.
The reason is due to the fact that the dependence of the
probabilities of interest on ![]() and
and ![]() is rather linear in the region where their probability
mass is concentrated, as shown in Fig.
is rather linear in the region where their probability
mass is concentrated, as shown in Fig. ![[*]](crossref.png) .
.

![[*]](crossref.png) : symmetric
variations of
: symmetric
variations of