Adding also the uncertainty about 
Now that we have learned the game, we can use it to
include also the uncertainty concerning  . At a given
stage of the pandemic we could have good reasons to
guess a proportion of infected around 10%, as we
have been done till now, with a sizable uncertainty,
for example 5% (i.e.
. At a given
stage of the pandemic we could have good reasons to
guess a proportion of infected around 10%, as we
have been done till now, with a sizable uncertainty,
for example 5% (i.e.
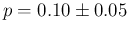 ). We model, also in this case,
). We model, also in this case,
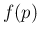 with a Beta distribution, getting
with a Beta distribution, getting 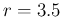 and
and 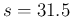 .
Equation (
.
Equation (![[*]](crossref.png) ) becomes then
) becomes then
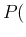 Inf Inf Pos Pos |
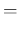 |
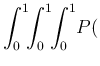 Inf Inf Pos Pos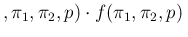 d d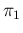 d d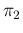 d d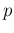 |
(41) |
| |
|
|
|
 |
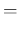 |
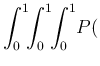 Inf Inf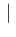 Pos Pos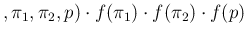 d d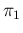 d d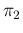 d d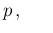 |
(42) |
in which we have made explicit that the joint pdf factorizes,
considering  ,
,  and
and  independent.25With a minor modification
to the script provided in Appendix B.126we get
independent.25With a minor modification
to the script provided in Appendix B.126we get
 Inf
Inf Pos
Pos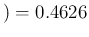 and
and
 NoInf
NoInf Neg
Neg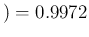 , reported again with an exaggerated number
of digits. We only note a small effect in
, reported again with an exaggerated number
of digits. We only note a small effect in
 Inf
Inf Pos
Pos .
As a further exercise, let also take into account
.
As a further exercise, let also take into account
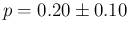 ,
modeled by a
Beta
,
modeled by a
Beta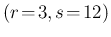 . In this case the Monte Carlo
integration yields
. In this case the Monte Carlo
integration yields
 Inf
Inf Pos
Pos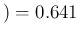 and
and
 NoInf
NoInf Neg
Neg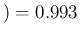 , to be compared with 0.682 and 0.994
of Tab.
, to be compared with 0.682 and 0.994
of Tab. ![[*]](crossref.png) .27
.27
![[*]](crossref.png) ) becomes then
) becomes then
![[*]](crossref.png) .27
.27