Next: Measurability of Up: Sampling a population Previous: Detailed study of the Contents
![[*]](crossref.png) ,
,
![[*]](crossref.png) and
and ![[*]](crossref.png) indicates the critical value
indicates the critical value
Being ![]() an important parameter in order to plan
a test campaign, it is worth getting its closed, although approximated
expression, obtained extending the
condition (
an important parameter in order to plan
a test campaign, it is worth getting its closed, although approximated
expression, obtained extending the
condition (![[*]](crossref.png) )
to
)
to
![[*]](crossref.png) )
can be neglected.38)
The top plot of Fig
)
can be neglected.38)
The top plot of Fig ![[*]](crossref.png) shows the dependence
of
shows the dependence
of 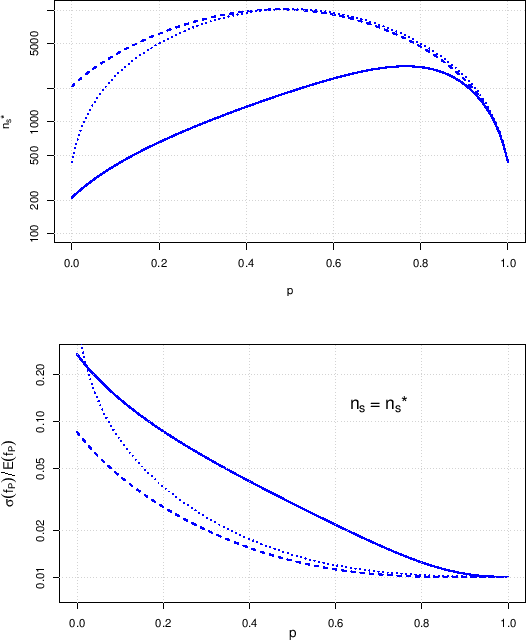 |
![[*]](crossref.png) and
and ![[*]](crossref.png) );
the improved case of
);
the improved case of
![[*]](crossref.png) and
and ![[*]](crossref.png) );
the mirror-symmetric case in which
E
);
the mirror-symmetric case in which
E![[*]](crossref.png) ).
Once we know the dependence of
).
Once we know the dependence of ![[*]](crossref.png) for the three cases of the upper plot of the same figure.
for the three cases of the upper plot of the same figure.
When we reduce the uncertainty about
![]() , keeping constant
its expected value, the systematic contribution to the uncertainty
is reduced and then, as we have already learned from
Figs.
, keeping constant
its expected value, the systematic contribution to the uncertainty
is reduced and then, as we have already learned from
Figs. ![[*]](crossref.png) ,
,
![[*]](crossref.png) and
and ![[*]](crossref.png) ,
it becomes meaningful to analyze larger samples.
We can then predict the fraction
of individuals tagged as positive with improved
accuracy, i.e.
,
it becomes meaningful to analyze larger samples.
We can then predict the fraction
of individuals tagged as positive with improved
accuracy, i.e.
![]() E
E![]() decreases.
This intuitive reasoning is confirmed by
the plots of Fig
decreases.
This intuitive reasoning is confirmed by
the plots of Fig ![[*]](crossref.png) , moving from the
solid curves to the dashed ones.
Instead, improving the specificity to 0.885
to 0.978, i.e. reducing
E
, moving from the
solid curves to the dashed ones.
Instead, improving the specificity to 0.885
to 0.978, i.e. reducing
E![]() from 0.115 to 0.022,
keeping the same uncertainty of 0.007,
leads to surprising results at low values of
from 0.115 to 0.022,
keeping the same uncertainty of 0.007,
leads to surprising results at low values of ![]() , at least at a first
sight (dashed curves
, at least at a first
sight (dashed curves
![]() dotted curves).
In fact, one would expect that from this further improvement
in the quality of the test (which definitively makes
a difference
when testing a single individual,
as discussed in Sec.
dotted curves).
In fact, one would expect that from this further improvement
in the quality of the test (which definitively makes
a difference
when testing a single individual,
as discussed in Sec. ![[*]](crossref.png) )
should follow a general improvement
in the prediction of the fraction of positives.
)
should follow a general improvement
in the prediction of the fraction of positives.
The reason of this counter-intuitive outcome
is due to the combination of two effects.
The first is the dependence on
E![]() and
E
and
E![]() of the statistical contributions to the
uncertainty, as we can see from Eqs. (
of the statistical contributions to the
uncertainty, as we can see from Eqs. (![[*]](crossref.png) ) and
(
) and
(![[*]](crossref.png) ). The second is that,
decreasing
E
). The second is that,
decreasing
E![]() , the expected value of
, the expected value of ![]() decreases too (less `false positives') and therefore
the relative uncertainty on
decreases too (less `false positives') and therefore
the relative uncertainty on ![]() , i.e.
, i.e.
![]() E
E![]() , increases.
While the second effect is rather obvious and there is
little to comment, we show the first one graphically,
for
, increases.
While the second effect is rather obvious and there is
little to comment, we show the first one graphically,
for ![]() at which the effects becomes sizable,
in the three plots of
Fig.
at which the effects becomes sizable,
in the three plots of
Fig. ![[*]](crossref.png) :
:
![[*]](crossref.png) ,
,
![[*]](crossref.png) and
and ![[*]](crossref.png) , these plots show
, these plots show
Summing up, the combination of the two plots of
Fig. ![[*]](crossref.png) gives at a glance,
for an assumed proportion of infectees
gives at a glance,
for an assumed proportion of infectees ![]() , an idea
of the `optimal' relative uncertainty we can get on
, an idea
of the `optimal' relative uncertainty we can get on ![]() (bottom plot)
and the sample size needed to achieve it (upper plot).
We remind that the lowest relative uncertainty, equal to
(bottom plot)
and the sample size needed to achieve it (upper plot).
We remind that the lowest relative uncertainty, equal to
![]() of the value shown in the plot, is reached
when the sample size
of the value shown in the plot, is reached
when the sample size ![]() is about one order of magnitude larger
than
is about one order of magnitude larger
than ![]() , i.e. when the random contribution to the uncertainty
is absolutely negligible and any further increase of
, i.e. when the random contribution to the uncertainty
is absolutely negligible and any further increase of ![]() not justifiable. But, anyway - think about it -
being
not justifiable. But, anyway - think about it -
being
![]() , is it worth increasing
so much (
, is it worth increasing
so much (
![]() times) the sample size in order
to reduce
times) the sample size in order
to reduce
![]() by only 30%?
by only 30%?