Now, after having seen what we can tell about a single
individual chosen at random and of which we have no information
about possible symptoms, contacts or behavior,
let us see what we can tell about
the proportion  of infected in the population, based
on the tests performed on the sampled individuals.
The first idea is to solve
Eqs. (
of infected in the population, based
on the tests performed on the sampled individuals.
The first idea is to solve
Eqs. (![[*]](crossref.png) ) and (
) and (![[*]](crossref.png) )
with respect to
)
with respect to  ,
from which it follows
,
from which it follows
Applying this formula to the 2060 positives got in our numerical
example we re-obtain the input proportion of 10%,
somehow getting reassured
about the correctness of the reasoning.
If, instead, we get more positives, for example 2500, 3000 or 3500,
then the proportion would rise to 15.1%, 20.1% and 26.7%, respectively,
which goes somehow in the `right direction'.
If, instead, we get less, for example 2000 or 1500, then the proportion
lowers to 9.3% and 3.5%, respectively, which also seems to go
into the right direction.
However, keeping lowering the number of positives something strange happens.
For 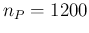 Eq. (
Eq. (![[*]](crossref.png) ) vanishes
and it becomes even negative for smaller numbers of positives,
which is something concerning,
indicating that the above formula
is not valid in general. But why did it nicely give the
exact result in the case of 2060 positives? And what is the reason
why it yields negative proportions below
1200 positives?
Moreover, Eq. (
) vanishes
and it becomes even negative for smaller numbers of positives,
which is something concerning,
indicating that the above formula
is not valid in general. But why did it nicely give the
exact result in the case of 2060 positives? And what is the reason
why it yields negative proportions below
1200 positives?
Moreover, Eq. (![[*]](crossref.png) ) has a worrying behavior of diverging
for
) has a worrying behavior of diverging
for
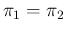 , even though irrelevant in practice, because such a test
would be ridiculous - the same as tossing a coin to tag a person
Positive or Negative (but in such a case we would expect to learn
nothing from the `test', certainly
not that the real proposition of infectees diverges!).
, even though irrelevant in practice, because such a test
would be ridiculous - the same as tossing a coin to tag a person
Positive or Negative (but in such a case we would expect to learn
nothing from the `test', certainly
not that the real proposition of infectees diverges!).
Let us see the limits of validity of the equation.
- The lower limit
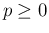 implies, as we have
already seen in the numerical
example,
implies, as we have
already seen in the numerical
example,
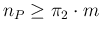 and
and
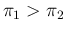 .9
.9
- The upper limit
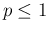 is reflected
in the condition
is reflected
in the condition
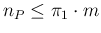 (and
(and
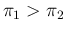 ).
In our numeric example this would mean to have less than 9800 positives
in our sample of 10000. But this ignores the fact that the
proportion of infectees in the sample could be higher than that
in the population.
).
In our numeric example this would mean to have less than 9800 positives
in our sample of 10000. But this ignores the fact that the
proportion of infectees in the sample could be higher than that
in the population.
Anyway, it is clear that when the model contemplates
probabilistic effects we have to use sound
methods based on probability theory.
![[*]](crossref.png) ) and (
) and (![[*]](crossref.png) )
with respect to
)
with respect to ![]() Eq. (
Eq. (![[*]](crossref.png) ) vanishes
and it becomes even negative for smaller numbers of positives,
which is something concerning,
indicating that the above formula
is not valid in general. But why did it nicely give the
exact result in the case of 2060 positives? And what is the reason
why it yields negative proportions below
1200 positives?
Moreover, Eq. (
) vanishes
and it becomes even negative for smaller numbers of positives,
which is something concerning,
indicating that the above formula
is not valid in general. But why did it nicely give the
exact result in the case of 2060 positives? And what is the reason
why it yields negative proportions below
1200 positives?
Moreover, Eq. (![[*]](crossref.png) ) has a worrying behavior of diverging
for
) has a worrying behavior of diverging
for
![]() , even though irrelevant in practice, because such a test
would be ridiculous - the same as tossing a coin to tag a person
Positive or Negative (but in such a case we would expect to learn
nothing from the `test', certainly
not that the real proposition of infectees diverges!).
, even though irrelevant in practice, because such a test
would be ridiculous - the same as tossing a coin to tag a person
Positive or Negative (but in such a case we would expect to learn
nothing from the `test', certainly
not that the real proposition of infectees diverges!).