The normalization factor 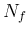 is given by the integral
in d
is given by the integral
in d of this expression, once
of this expression, once 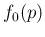 has been chosen.
As we have done in the previous section, we opt for
Beta
has been chosen.
As we have done in the previous section, we opt for
Beta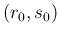 ,
taking the advantage not only of the flexibility
of the probability distribution to model our `prior
judgment' on
,
taking the advantage not only of the flexibility
of the probability distribution to model our `prior
judgment' on  , but also of its mathematical
convenience. In fact, with this choice, the resulting term
in Eq. (
, but also of its mathematical
convenience. In fact, with this choice, the resulting term
in Eq. (![[*]](crossref.png) ) depending on
) depending on  is given
by
is given
by
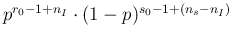 . The integral
over
. The integral
over  from 0 to 1 yields again a Beta function, that is
B
from 0 to 1 yields again a Beta function, that is
B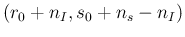 , thus
getting
, thus
getting
Similarly, we can evaluate
the expression of the expected values of  and of
and of 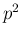 ,
from which the variance follows, being
,
from which the variance follows, being
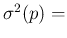 E
E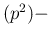 E
E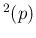 . For example,
being
E
. For example,
being
E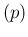 given by
given by
in the integral the term depending on  becomes
becomes
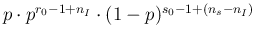 ,
increasing the power of
,
increasing the power of  by 1 and
thus yielding
by 1 and
thus yielding
while
E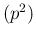 is obtained replacing `
is obtained replacing `
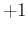 ' by
`
' by
`
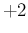 '. A script to evaluate expected value and standard deviation
of
'. A script to evaluate expected value and standard deviation
of  is provided in Appendix B.13.
is provided in Appendix B.13.
The expression can be extended to `
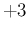 ' by `
' by `
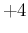 ',
thus getting
E
',
thus getting
E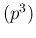 and
E
and
E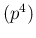 , from which
skewness and kurtosis can be evaluated.
Finally, making use of the so called
Pearson Distribution System implemented in R [14],
, from which
skewness and kurtosis can be evaluated.
Finally, making use of the so called
Pearson Distribution System implemented in R [14],
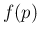 can be obtained with a quite high degree of accuracy, unless
the distribution is squeezed towards 0 o 1, as
e.g. in Fig.
can be obtained with a quite high degree of accuracy, unless
the distribution is squeezed towards 0 o 1, as
e.g. in Fig. ![[*]](crossref.png) .57 A script to evaluate mean, variance, skewness and kurtosis, and
from them
.57 A script to evaluate mean, variance, skewness and kurtosis, and
from them 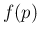 by the Pearson Distribution System is shown
in Appendix B.14.
by the Pearson Distribution System is shown
in Appendix B.14.
![[*]](crossref.png) ) depending on
) depending on 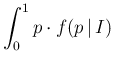 d
d![]() ' by `
' by `
![]() ',
thus getting
E
',
thus getting
E![]() and
E
and
E![]() , from which
skewness and kurtosis can be evaluated.
Finally, making use of the so called
Pearson Distribution System implemented in R [14],
, from which
skewness and kurtosis can be evaluated.
Finally, making use of the so called
Pearson Distribution System implemented in R [14],
![]() can be obtained with a quite high degree of accuracy, unless
the distribution is squeezed towards 0 o 1, as
e.g. in Fig.
can be obtained with a quite high degree of accuracy, unless
the distribution is squeezed towards 0 o 1, as
e.g. in Fig. ![[*]](crossref.png) .57 A script to evaluate mean, variance, skewness and kurtosis, and
from them
.57 A script to evaluate mean, variance, skewness and kurtosis, and
from them ![]() by the Pearson Distribution System is shown
in Appendix B.14.
by the Pearson Distribution System is shown
in Appendix B.14.