Next: Normalization factor and other Up: Exact evaluation of Previous: Exact evaluation of Contents
![[*]](crossref.png) , the inference
of the `unobserved' variables, based on the `observed' one,
for the problem represented graphically in the `Bayesian'
network of Fig.
, the inference
of the `unobserved' variables, based on the `observed' one,
for the problem represented graphically in the `Bayesian'
network of Fig. ![[*]](crossref.png) , consists
in evaluating `somehow'
, consists
in evaluating `somehow'
![[*]](crossref.png) ) is proportional to Eq. (
) is proportional to Eq. (![[*]](crossref.png) ),
hereafter indicated by `
),
hereafter indicated by `![[*]](crossref.png) :
:
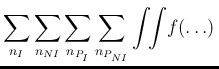 d d |
As a first step we simplify the equation by summing
over
![]() and
and ![]() and exploiting the Kroneker delta
terms (
and exploiting the Kroneker delta
terms (![[*]](crossref.png) ) and (
) and (![[*]](crossref.png) ).
We can then replace
).
We can then replace
![]() with
with
![]() and
and ![]() with
with ![]()
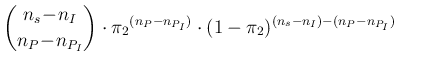 |
(96) |
The inferential distribution of interest
![]() ,
becomes then, besides constant factors and indicating
all the status of information on which the inference is based
as `
,
becomes then, besides constant factors and indicating
all the status of information on which the inference is based
as `![]() ', that is
', that is
![]() ,
,
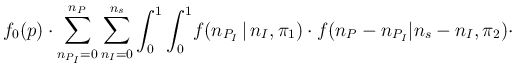 |
|||
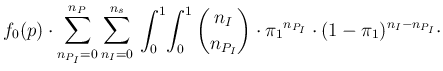 |
|||
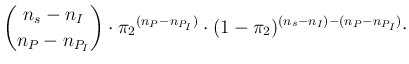 |
|||
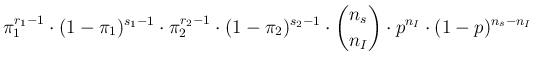 d d |
The two integrals appearing
in Eq. (![[*]](crossref.png) ) are, in terms of the generic variable
) are, in terms of the generic variable ![]() ,
of the form
,
of the form
![]() d
d![]() ,
which defines the special function beta
B
,
which defines the special function beta
B![]() ,
whose value
can be expressed
in terms of Gamma function as
B
,
whose value
can be expressed
in terms of Gamma function as
B![]() .
We get then
.
We get then