Although Monte Carlo integration is a powerful tool to solve
at best non trivial problems of this kind, it is
very useful to get, whenever it is possible, approximate solutions
in order to have an idea, analyzing the resulting formulae,
of how the result depends on the assumptions.
First at all, in analogy to what we have seen in
Sec. ![[*]](crossref.png) , we can be rather confident
that the expected value of
, we can be rather confident
that the expected value of 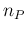 is not
significantly affected, as also
confirmed by the Monte Carlo results shown in Fig.
is not
significantly affected, as also
confirmed by the Monte Carlo results shown in Fig. ![[*]](crossref.png) .
The variance, given by Eq. (
.
The variance, given by Eq. (![[*]](crossref.png) )
is, instead, increased by terms
whose approximated values can be obtained by
linearization.29These are the resulting approximated expressions:30
)
is, instead, increased by terms
whose approximated values can be obtained by
linearization.29These are the resulting approximated expressions:30
Applying them to the case shown in Fig. ![[*]](crossref.png) we obtain an expected value of 2013
and a standard deviation of 200, in excellent agreement
with the Monte Carlo result.
In order to have an idea of the deviation from `normality'
we also over-impose,
to the bottom histogram of the figure, the Gaussian
having average and standard deviation
calculated by Eq. (
we obtain an expected value of 2013
and a standard deviation of 200, in excellent agreement
with the Monte Carlo result.
In order to have an idea of the deviation from `normality'
we also over-impose,
to the bottom histogram of the figure, the Gaussian
having average and standard deviation
calculated by Eq. (![[*]](crossref.png) ) and (
) and (![[*]](crossref.png) )
- we remind that the top histogram has instead strong
theoretical reasons to be, with
very good approximation, normally distributed
(a zoomed version of the same histogram is reported
in Fig.
)
- we remind that the top histogram has instead strong
theoretical reasons to be, with
very good approximation, normally distributed
(a zoomed version of the same histogram is reported
in Fig. ![[*]](crossref.png) ).
).
As a further check, let us see what happens
in the case of no infected individuals in the sample, that is  .
The Monte Carlo results
are shown in Fig.
.
The Monte Carlo results
are shown in Fig. ![[*]](crossref.png) ,
,
Figure:
Same as Fig. ![[*]](crossref.png) , but in the
case of no infected individual in the sample (
, but in the
case of no infected individual in the sample ( ).
The over-imposed Gaussian has average
1150 and standard deviation 222.
).
The over-imposed Gaussian has average
1150 and standard deviation 222.
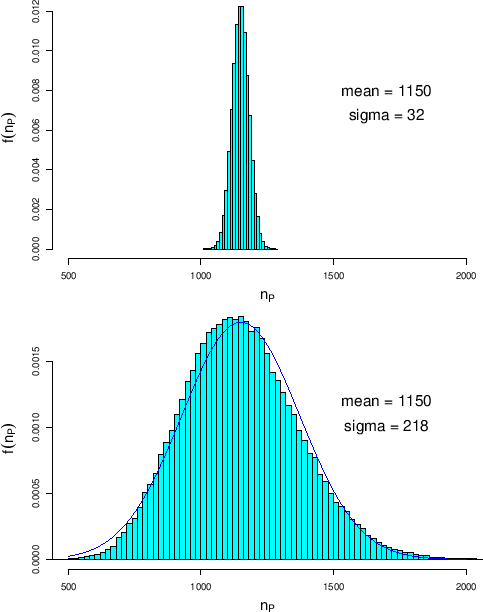 |
We see that, as already stated qualitatively in Sec. ![[*]](crossref.png) ,
number of positives can occur well below the value one would compute
only reasoning on rough estimates (1150 in this case).
Therefore, since the formulae derived in that way were unreliable,
a probabilistic treatment
of the problem is needed in order to take into account the fact
that fluctuations around expected values do usually occur.
Also in this case the approximated results obtained by
Eqs. (
,
number of positives can occur well below the value one would compute
only reasoning on rough estimates (1150 in this case).
Therefore, since the formulae derived in that way were unreliable,
a probabilistic treatment
of the problem is needed in order to take into account the fact
that fluctuations around expected values do usually occur.
Also in this case the approximated results obtained by
Eqs. (![[*]](crossref.png) ) and (
) and (![[*]](crossref.png) )
are in excellent agreement with the Monte Carlo estimates,
yielding
)
are in excellent agreement with the Monte Carlo estimates,
yielding
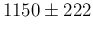 (and, again, the Gaussian approximation
is not too bad, at least within
a couple of standard deviations from the mean value).
The approximation remains good also for high values
of
(and, again, the Gaussian approximation
is not too bad, at least within
a couple of standard deviations from the mean value).
The approximation remains good also for high values
of  . For example, for the quite high value of
. For example, for the quite high value of 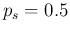 , the Monte Carlo
integration gives
, the Monte Carlo
integration gives
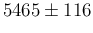 versus an approximated result
of
versus an approximated result
of
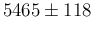 .
.
A natural question is how the results change not only with
the proportion of infectees in the sample,
but also with the size of the sample. The answer
is given in Tab. ![[*]](crossref.png) , with
, with 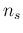 varying,
in steps of roughly half order of magnitude,
from the ridiculous value of 100 up to 100000
(that is
varying,
in steps of roughly half order of magnitude,
from the ridiculous value of 100 up to 100000
(that is
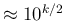 , with
, with
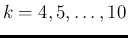 ).
).
Table:
Predicted fraction of tagged positives
in a sample (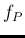 ) as a function of the assumed proportion
of infected individuals in the sample (
) as a function of the assumed proportion
of infected individuals in the sample ( ), also
taking into account the uncertainty on the test
parameters
), also
taking into account the uncertainty on the test
parameters  and
and  (numbers in squared brackets -
those in round brackets are evaluated at the expected values
of
(numbers in squared brackets -
those in round brackets are evaluated at the expected values
of  and
and  ).
).
 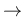 |
0.01 |
0.05 |
0.10 |
0.15 |
0.20 |
0.50 |
E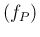 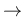 |
0.124 |
0.158 |
0.201 |
0.244 |
0.287 |
0.546 |
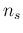 : : |
standard uncertainties |
|
100
|
(0.032) |
(0.031) |
(0.031) |
(0.030) |
(0.029) |
(0.025) |
|
|
[0.038] |
[0.037] |
[0.036] |
[0.035] |
[0.034] |
[0.027] |
|
300
|
(0.018) |
(0.018) |
(0.018) |
(0.017) |
(0.017) |
(0.014) |
|
|
[0.028] |
[0.027] |
[0.026] |
[0.025] |
[0.024] |
[0.018] |
|
1000
|
(0.010) |
(0.010) |
(0.010) |
(0.009) |
(0.009) |
(0.008) |
|
|
[0.024] |
[0.023] |
[0.022] |
[0.021] |
[0.020] |
[0.014] |
|
3000
|
(0.006) |
(0.006) |
(0.006) |
(0.005) |
(0.005) |
(0.005) |
|
|
[0.022] |
[0.021] |
[0.020] |
[0.019] |
[0.018] |
[0.012] |
|
10000
|
(0.003) |
(0.003) |
(0.003) |
(0.003) |
(0.003) |
(0.002) |
|
|
[0.022] |
[0.021] |
[0.020] |
[0.019] |
[0.018] |
[0.012] |
|
30000
|
(0.002) |
(0.002) |
(0.002) |
(0.002) |
(0.002) |
(0.001) |
|
|
[0.021] |
[0.021] |
[0.020] |
[0.018] |
[0.017] |
[0.011] |
|
100000
|
(0.001) |
(0.001) |
(0.001) |
(0.001) |
(0.001) |
(0.001) |
|
|
[0.021] |
[0.021] |
[0.019] |
[0.018] |
[0.017] |
[0.011] |
|
The chosen values of  are the same of
are the same of  of
Tab.
of
Tab. ![[*]](crossref.png) . For an easier comparison,
the fraction
. For an easier comparison,
the fraction 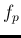 of positively tagged individual
is provided.
The expected value of
of positively tagged individual
is provided.
The expected value of 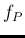 , depending essentially
only on
, depending essentially
only on  , is reported in the second row of the table.
Two standard uncertainties are reported for each combination
of
, is reported in the second row of the table.
Two standard uncertainties are reported for each combination
of  and
and 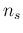 : the first, in round brackets, only takes
into account the two binomial distributions (`statistical errors',
in old style31physicist's jargon); the second, in square brackets takes
into account also the possible variability of
: the first, in round brackets, only takes
into account the two binomial distributions (`statistical errors',
in old style31physicist's jargon); the second, in square brackets takes
into account also the possible variability of  and
and  (`systematic error', in the same jargon). They have all been evaluated
by Monte Carlo, but the agreement with the approximated formula
(
(`systematic error', in the same jargon). They have all been evaluated
by Monte Carlo, but the agreement with the approximated formula
(![[*]](crossref.png) ) has been
checked.
) has been
checked.
![[*]](crossref.png) , we can be rather confident
that the expected value of
, we can be rather confident
that the expected value of ![[*]](crossref.png) .
The variance, given by Eq. (
.
The variance, given by Eq. (![[*]](crossref.png) )
is, instead, increased by terms
whose approximated values can be obtained by
linearization.29These are the resulting approximated expressions:30
)
is, instead, increased by terms
whose approximated values can be obtained by
linearization.29These are the resulting approximated expressions:30
![[*]](crossref.png) we obtain an expected value of 2013
and a standard deviation of 200, in excellent agreement
with the Monte Carlo result.
In order to have an idea of the deviation from `normality'
we also over-impose,
to the bottom histogram of the figure, the Gaussian
having average and standard deviation
calculated by Eq. (
we obtain an expected value of 2013
and a standard deviation of 200, in excellent agreement
with the Monte Carlo result.
In order to have an idea of the deviation from `normality'
we also over-impose,
to the bottom histogram of the figure, the Gaussian
having average and standard deviation
calculated by Eq. (![[*]](crossref.png) ) and (
) and (![[*]](crossref.png) )
- we remind that the top histogram has instead strong
theoretical reasons to be, with
very good approximation, normally distributed
(a zoomed version of the same histogram is reported
in Fig.
)
- we remind that the top histogram has instead strong
theoretical reasons to be, with
very good approximation, normally distributed
(a zoomed version of the same histogram is reported
in Fig. ![[*]](crossref.png) ).
).
![]() .
The Monte Carlo results
are shown in Fig.
.
The Monte Carlo results
are shown in Fig. ![[*]](crossref.png) ,
,

![[*]](crossref.png) ,
number of positives can occur well below the value one would compute
only reasoning on rough estimates (1150 in this case).
Therefore, since the formulae derived in that way were unreliable,
a probabilistic treatment
of the problem is needed in order to take into account the fact
that fluctuations around expected values do usually occur.
Also in this case the approximated results obtained by
Eqs. (
,
number of positives can occur well below the value one would compute
only reasoning on rough estimates (1150 in this case).
Therefore, since the formulae derived in that way were unreliable,
a probabilistic treatment
of the problem is needed in order to take into account the fact
that fluctuations around expected values do usually occur.
Also in this case the approximated results obtained by
Eqs. (![[*]](crossref.png) ) and (
) and (![[*]](crossref.png) )
are in excellent agreement with the Monte Carlo estimates,
yielding
)
are in excellent agreement with the Monte Carlo estimates,
yielding
![[*]](crossref.png) , with
, with ![]() varying,
in steps of roughly half order of magnitude,
from the ridiculous value of 100 up to 100000
(that is
varying,
in steps of roughly half order of magnitude,
from the ridiculous value of 100 up to 100000
(that is
![]() , with
, with
![]() ).
).
![[*]](crossref.png) . For an easier comparison,
the fraction
. For an easier comparison,
the fraction ![[*]](crossref.png) ) has been
checked.
) has been
checked.