Since we cannot go into indefinite and sterile discussions
on all the possible priors that we might use
(remember that if we collect and analyze data is to improve our knowledge,
often used to make practical decision in a finite time scale!)
it is important to understand a bit deeper their role in the inference.
This can be done
factorizing Eq. (![[*]](crossref.png) ), written here
in compact notation as
), written here
in compact notation as
into two parts:
one that only contains
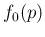 and the other containing the remaining factors of the `chain',
indicated here as
and the other containing the remaining factors of the `chain',
indicated here as
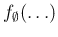 :
:
The unnormalized pdf of  , conditioned by data and parameters,
can be then rewritten (see Appendix A) as
, conditioned by data and parameters,
can be then rewritten (see Appendix A) as
in which we have indicated with the usual symbol used
for the (`integrated') likelihood
(in which constant factors are irrelevant)
the part which multiplies 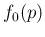 .
It is then rather evident the role of
.
It is then rather evident the role of  in
`reshaping'
in
`reshaping' 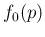 .53In the particular case in which
.53In the particular case in which 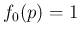 the inference
is simply given by
the inference
is simply given by
(“the inference is determined by the likelihood”).
If, instead, the prior is not flat, then it does reshape
the posterior obtained by 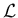 alone.
Therefore there are two alternative
ways to see the contributions
of
alone.
Therefore there are two alternative
ways to see the contributions
of 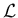 and
and 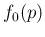 : each one reshapes the other.
In particular
: each one reshapes the other.
In particular
- in the regions of
 set to zero by either function
the posterior vanishes;
set to zero by either function
the posterior vanishes;
- the function which is more narrow around its maximum
`wins' against the smoother one.
Therefore, for the case shown in Fig. ![[*]](crossref.png) ,
obtained by a flat prior, the `density of
,
obtained by a flat prior, the `density of  '
is nothing but the shape of
'
is nothing but the shape of
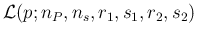 .
If
.
If 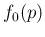 is constant, or varies slowly, in the range
is constant, or varies slowly, in the range
![$[0.02,0.17]$](img808.png) it provides null or little effect. If, instead, it is very peaked
around 0.15 (e.g. with a standard deviation of
it provides null or little effect. If, instead, it is very peaked
around 0.15 (e.g. with a standard deviation of
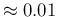 )
it dominates the inference.
)
it dominates the inference.
But what is more interesting is that the reshape
by 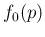 can be done in a second step.54This is the importance of choosing a flat prior
(and not just a question of laziness): the data analysis expert
could then present a result of the kind
of Fig.
can be done in a second step.54This is the importance of choosing a flat prior
(and not just a question of laziness): the data analysis expert
could then present a result of the kind
of Fig. ![[*]](crossref.png) to an epidemiologist who could then
reshape her priors (or, equivalently, reshape the curve provided
by the data analyst with her priors).
But she could also have such a strong prior on the variable under study,
that she could reject tout court the result, blaming the
data analysis expert that there must be something wrong in
the analysis or in the data - see Sec.
to an epidemiologist who could then
reshape her priors (or, equivalently, reshape the curve provided
by the data analyst with her priors).
But she could also have such a strong prior on the variable under study,
that she could reject tout court the result, blaming the
data analysis expert that there must be something wrong in
the analysis or in the data - see Sec. ![[*]](crossref.png) .
.
![[*]](crossref.png) ), written here
in compact notation as
), written here
in compact notation as
![$\displaystyle \left[ \sum_{n_I}\sum_{n_{NI}}\sum_{n_{P_I}}\sum_{n_{P_{NI}}}
\in...
...tyset}(\ldots)\,\mbox{d}\pi_1
\mbox{d}\pi_2\right]\! \cdot f_0(p) \ \ \ \mbox{}$](img796.png)
![]() alone.
Therefore there are two alternative
ways to see the contributions
of
alone.
Therefore there are two alternative
ways to see the contributions
of ![]() and
and ![]() : each one reshapes the other.
In particular
: each one reshapes the other.
In particular
![[*]](crossref.png) ,
obtained by a flat prior, the `density of
,
obtained by a flat prior, the `density of ![]() can be done in a second step.54This is the importance of choosing a flat prior
(and not just a question of laziness): the data analysis expert
could then present a result of the kind
of Fig.
can be done in a second step.54This is the importance of choosing a flat prior
(and not just a question of laziness): the data analysis expert
could then present a result of the kind
of Fig. ![[*]](crossref.png) to an epidemiologist who could then
reshape her priors (or, equivalently, reshape the curve provided
by the data analyst with her priors).
But she could also have such a strong prior on the variable under study,
that she could reject tout court the result, blaming the
data analysis expert that there must be something wrong in
the analysis or in the data - see Sec.
to an epidemiologist who could then
reshape her priors (or, equivalently, reshape the curve provided
by the data analyst with her priors).
But she could also have such a strong prior on the variable under study,
that she could reject tout court the result, blaming the
data analysis expert that there must be something wrong in
the analysis or in the data - see Sec. ![[*]](crossref.png) .
.