Next: Exact evaluation of Up: Which priors? Previous: Some examples Contents
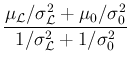 |
(86) | ||
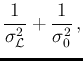 |
(87) |
![[*]](crossref.png) ,
for which
,
for which
![[*]](crossref.png) . The idea is to see the pdf
estimated by JAGS with flat prior as a `rough Beta'
whose parameters can be estimated from the mean and the standard deviation
using Eqs. (
. The idea is to see the pdf
estimated by JAGS with flat prior as a `rough Beta'
whose parameters can be estimated from the mean and the standard deviation
using Eqs. (![[*]](crossref.png) )-(
)-(![[*]](crossref.png) ).
We can then imagine that the pdf of
).
We can then imagine that the pdf of ![[*]](crossref.png) )-(
)-(![[*]](crossref.png) ).
The trick consists then in modifying the Beta parameters
according to the simple rules:
).
The trick consists then in modifying the Beta parameters
according to the simple rules:
![[*]](crossref.png) ) and (
) and (![[*]](crossref.png) ).
Then the new mean and standard deviation are evaluated from
).
Then the new mean and standard deviation are evaluated from ![[*]](crossref.png) ).
).
For example, in the case of Fig. ![[*]](crossref.png) we have (with an exaggerated number of digits)
we have (with an exaggerated number of digits)
![]() , which could derive from a Beta
having
, which could derive from a Beta
having
![]() and
and
![]() .
If we have a prior somehow peaked around 0.3, e.g.
.
If we have a prior somehow peaked around 0.3, e.g.
![]() , it can be parameterized by a Beta with
, it can be parameterized by a Beta with ![]() and
and ![]() . Applying the above rule we get
. Applying the above rule we get