Contribution of the uncertainty on due to sampling

Including in the approximated formulae the contribution of the uncertainty on due to sampling

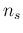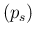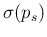Next section will be dedicated to the effect of sampling individuals from a population. However, having taken some confidence with the approximated formulae, we can already extend them in order to see how the uncertain , characterized by its expected value E and standard uncertainty $\sigma(p_s)$ , whose evaluation will be the subject of Sec.

, affects our prediction about the number of individuals resulting positive in the test. In the approximated expression for the expected value of 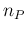(Eq.

) we have to replace by its expected value E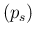, while in the variance we have to add a term again obtained by linearization,³³ thus getting

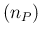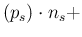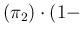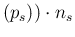E $\displaystyle (n_P)$	$\displaystyle \approx$	E $\displaystyle (\pi_1)\cdot$ E $\displaystyle (p_s)\cdot n_s +$ E $\displaystyle (\pi_2)\cdot (1-$ E $\displaystyle (p_s))\cdot n_s$	(57)
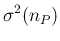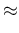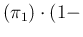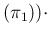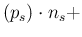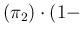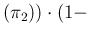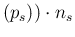$\displaystyle \sigma^2(n_P)$	$\displaystyle \approx$	E $\displaystyle (\pi_1)\cdot (1-$ E $\displaystyle (\pi_1)) \cdot$ E $\displaystyle (p_s)\cdot n_s +$ E $\displaystyle (\pi_2)\cdot (1-$ E $\displaystyle (\pi_2))\cdot (1-$ E $\displaystyle (p_s))\cdot n_s$
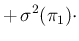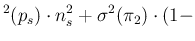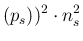		$\displaystyle + \,\sigma^2(\pi_1)\cdot$ E $\displaystyle ^2(p_s)\cdot n_s^2 + \sigma^2(\pi_2)\cdot (1-$ E $\displaystyle (p_s))^2\cdot n_s^2$
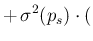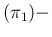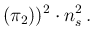		$\displaystyle + \,\sigma^2(p_s)\cdot ($ E $\displaystyle (\pi_1) -$ E $\displaystyle (\pi_2))^2\cdot n_s^2\,.$	(58)

As far as the fraction of positives is concerned, we have the following four contributions to the global uncertainty,

$\displaystyle \sigma(f_P)$

$\displaystyle \approx$

$\displaystyle \sigma_R(f_P) \oplus \sigma_{\pi_1}(f_P) \oplus \sigma_{\pi_2}(f_P) \oplus \sigma_{p_s}(f_P) \,,$

(59)

the first three given by Eqs. (

), in which has to be replaced by its expected value E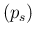, and the fourth term being

$\displaystyle \sigma_{p_s}(f_P)$

$\displaystyle =$

$\displaystyle \sigma(p_s)\cdot \vert$ E $\displaystyle (\pi_1) -$ E $\displaystyle (\pi_2)\vert\,.$

(60)

(Note that also the fourth term is of `random nature', although, from the `perspective' we are now seeing the problem it could be considered as a third contribution to systematics.³⁴)