Conclusions
In this paper we went through the issues of `stating'
if an individual belong to a particular class
and in `counting' the number of individuals in a population
belonging to that class.
Since the casus belli was the Covid-19 pandemic,
we have been constantly speaking of (currently and past)
`infectees', although our work is rather general.
A well understood complication related to the above tasks
is due to the fact that the assignment of an individual to
the class of interest is performed by 'proxies'
provided by the test result,
in this case `positive' or `negative'.
Having defined  the probability that
the test result gives positive if the individual
is infected (`sensitivity') and
the probability that
the test result gives positive if the individual
is infected (`sensitivity') and  the probability of positive if not infected
(
the probability of positive if not infected
(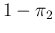 being the `specificity'),
we have analyzed the impact on the results
of the fact that not only these `test parameters' are
far from being ideal (
being the `specificity'),
we have analyzed the impact on the results
of the fact that not only these `test parameters' are
far from being ideal (
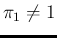 and
and
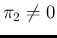 ),
but that their values are indeed uncertain.
),
but that their values are indeed uncertain.
We have started our work using parameters that can be
summarized as
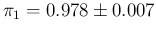 and
and
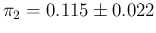 ,
based on the nominal data provided by Ref. [16] (
,
based on the nominal data provided by Ref. [16] (
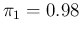 and
and
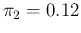 ),
and used probability theory, and in particular
the so called Bayes' rule, in order to
),
and used probability theory, and in particular
the so called Bayes' rule, in order to
- evaluate the probability that an individual declared
positive is infected (and so on for the other possibilities);
- evaluate the proportion of infectees in a population,
based on the number of positive in a tested sample.
In both problems the role of `priors' is logically crucial,
although in practice it has a different impact on the numerical result:
- the probability that an individual tagged
as positive is infected depends strongly on the probability
of being infected based on other pieces of information
and knowledge (in the idealistic case of `zero knowledge'
this prior probability is just the assumed proportion of infectees
in the population);
- the probability density function of the proportion of infectees in the
population has, instead, usually a weak dependence
on the prior beliefs about the same proportion.
The dependence on the fact that the tests are `imperfect' has
a different impact on the result:
- the probability of infected if positive depends strongly,
as expected, on the values
(`expected values', in probabilistic terms)
of
 and
and  , while, rather surprisingly,
it depends very little on their
uncertainty;
, while, rather surprisingly,
it depends very little on their
uncertainty;
- the inference of the proportion of infectees, instead,
depends strongly on their uncertainty, but very little on their expected values.
The latter outcome is important for planning test campaigns to
count and regularly monitor the number of infectees in a population,
for which tests with relatively low sensitivity and specificity
can be employed. This second task has been analyzed in detail
by exact evaluations, Monte Carlo methods and approximated formulae,
first to understand the accuracy of the predictions of the number of
positives that would result in a sample of the population,
assuming a given proportion of infectees in the population;
then to infer the proportion of infectees in the population
from the observed number of positives.
The preliminary work of predicting the number of positives has been
particularly important because it has allowed us to produce
approximated formulae with which we can disentangle the
contributions to the overall uncertainty of prediction,
which has a somehow specular relation with the uncertainty in inference.
This allows to classify then the contributions
into 'statistics' (those depending on the
sample size, due to the probabilistic effects of sampling)
and `systematics' (those not depending on the sample
size, due then to the uncertainties on  and
and  ).
As a consequence it is possible to evaluate the critical sample size,
above which uncertainties due to systematics are dominant, and therefore it is not worth
increasing the sample size.
).
As a consequence it is possible to evaluate the critical sample size,
above which uncertainties due to systematics are dominant, and therefore it is not worth
increasing the sample size.
Moreover, the fact that the uncertainties about  and
and  act as systematics (within the limitation of our model,
clearly stated in Sec.
act as systematics (within the limitation of our model,
clearly stated in Sec. ![[*]](crossref.png) )
suggests that we can evaluate differences of proportions of infectees in
different populations much better than how we can measure a single proportion.
This observation has an important practical consequence, because
one could measure the proportion of infectees in a subpopulation
(think e.g. to a Region of a Country) both
with a test of higher quality (and presumably more expensive) and with a cheaper, rapid and less accurate one
and therefore use the result as calibration point for the other subpopulations.
)
suggests that we can evaluate differences of proportions of infectees in
different populations much better than how we can measure a single proportion.
This observation has an important practical consequence, because
one could measure the proportion of infectees in a subpopulation
(think e.g. to a Region of a Country) both
with a test of higher quality (and presumably more expensive) and with a cheaper, rapid and less accurate one
and therefore use the result as calibration point for the other subpopulations.
![]() and
and
![]() ,
based on the nominal data provided by Ref. [16] (
,
based on the nominal data provided by Ref. [16] (
![]() and
and
![]() ),
and used probability theory, and in particular
the so called Bayes' rule, in order to
),
and used probability theory, and in particular
the so called Bayes' rule, in order to
![]() and
and ![]() ).
As a consequence it is possible to evaluate the critical sample size,
above which uncertainties due to systematics are dominant, and therefore it is not worth
increasing the sample size.
).
As a consequence it is possible to evaluate the critical sample size,
above which uncertainties due to systematics are dominant, and therefore it is not worth
increasing the sample size.
![]() and
and ![]() act as systematics (within the limitation of our model,
clearly stated in Sec.
act as systematics (within the limitation of our model,
clearly stated in Sec. ![[*]](crossref.png) )
suggests that we can evaluate differences of proportions of infectees in
different populations much better than how we can measure a single proportion.
This observation has an important practical consequence, because
one could measure the proportion of infectees in a subpopulation
(think e.g. to a Region of a Country) both
with a test of higher quality (and presumably more expensive) and with a cheaper, rapid and less accurate one
and therefore use the result as calibration point for the other subpopulations.
)
suggests that we can evaluate differences of proportions of infectees in
different populations much better than how we can measure a single proportion.
This observation has an important practical consequence, because
one could measure the proportion of infectees in a subpopulation
(think e.g. to a Region of a Country) both
with a test of higher quality (and presumably more expensive) and with a cheaper, rapid and less accurate one
and therefore use the result as calibration point for the other subpopulations.