Let us start with just two experimental outcomes,10 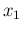 and
and 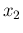 , resulting from the
uncertain `true' value
, resulting from the
uncertain `true' value 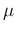 (what we are interested in)
when measured in two independent experiments having Gaussian
error functions with standard deviations
(what we are interested in)
when measured in two independent experiments having Gaussian
error functions with standard deviations 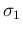 and
and 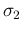 ,
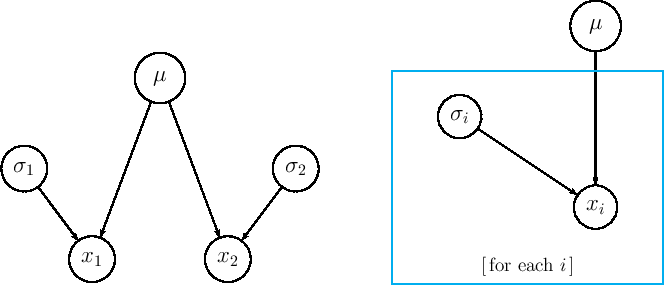
as sketched in the left hand graph of Fig. 5.
,
as sketched in the left hand graph of Fig. 5.
Figure:
Graphical model behind the standard combination.
 |
That is
The general case, with many measurements of the same 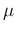 ,
is shown on the right hand graph of the same figure.
From a probabilistic point of view our aim will be to
assess, with a probability distribution, the intervals
where we believe
,
is shown on the right hand graph of the same figure.
From a probabilistic point of view our aim will be to
assess, with a probability distribution, the intervals
where we believe 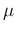 lies with different probabilities,
that is to arrive to
lies with different probabilities,
that is to arrive to
The pdf of interest can be (in principle) obtained easily
if we knew the joint pdf of all the quantities of interest,
that is
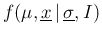 . In fact,
we just need to apply
a well know general rule of probability theory
(remember that in this first example
the
. In fact,
we just need to apply
a well know general rule of probability theory
(remember that in this first example
the 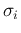 are just fixed conditions, although in general
they might become subject to inference too, as we shall see later):
are just fixed conditions, although in general
they might become subject to inference too, as we shall see later):
At this point the reader might be scared by two reasons:
the first is how to build up the joint pdf
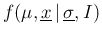 ;
the second is how to perform the integral over
;
the second is how to perform the integral over 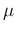 (`marginalization')
in order to get the denominator.11
(`marginalization')
in order to get the denominator.11
The first good news is that, given the model
(those of Fig. 5 or the more complicate ones
we shall see later), the denominator is just a number,
in general difficult to calculate, but just a number. This means
that we can rewrite the previous equation as
As next step, we can follow two strategies:
- calculate the normalization factor at the end, either
analytically or numerically;
- sample the unnormalized distribution by Monte Carlo
techniques, in order to get the shape of
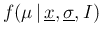 and to calculate
all moments of interest.
and to calculate
all moments of interest.
The second good news is that the multidimensional joint pdf
can be easily written down using the well known
probability theory theorem known as
chain rule. Indeed, sticking to the model with just two
variables, we can apply the chain rule in different ways.
For example,
beginning from the most pedantic one, we have
But this writing does not help us,
since it requires
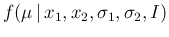 , which it is
precisely what we aim for.
It is indeed much better, with an eye to
Fig. 5, a bottom up approach (in the following
equation the order of the arguments in the left side term
has been changed to make the correspondence
between the two writings easier), that is
, which it is
precisely what we aim for.
It is indeed much better, with an eye to
Fig. 5, a bottom up approach (in the following
equation the order of the arguments in the left side term
has been changed to make the correspondence
between the two writings easier), that is
This equation can be
further simplified if we note that each 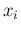 depends
directly only on
depends
directly only on 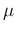 and
and 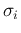 , while
, while
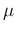 does not depend (at least in usual measurements)
on
does not depend (at least in usual measurements)
on 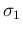 and
and 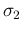 . We get then
. We get then
We can easily generalize this equation, in the case of many observations
described in the right hand graph of Fig. 5,
rewriting it as
where the index 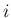 runs through all the observations
and the symbol `
runs through all the observations
and the symbol `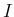 ' indicating the background state of information
has been dropped, using `
' indicating the background state of information
has been dropped, using `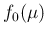 '
for the initial distribution (`prior') of
'
for the initial distribution (`prior') of 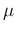 .
Finally, taking (for the moment)
for
.
Finally, taking (for the moment)
for 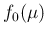 a
practically flat distribution in the region of interest
(see footnote 9), making use of
Eq. (3) and of the symbol
a
practically flat distribution in the region of interest
(see footnote 9), making use of
Eq. (3) and of the symbol 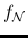 to indicate normal (i.e. Gaussian) error functions,
we get
to indicate normal (i.e. Gaussian) error functions,
we get
Using the explicit expression of the Gaussian and neglecting
all multiplicative factors that do not depend on 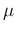 ,
we get
,
we get
where
Note that the mean of the squares
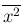 has been taken out of the exponent
has been taken out of the exponent
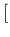 step from Eq. (8) to Eq. (9)
step from Eq. (8) to Eq. (9) ![$]$](img27.png) because
because
![$\exp[-\overline{x^2}/(2\sigma_C^2)]$](img101.png) does not depend on
does not depend on 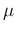 and therefore it can be absorbed in the normalization constant.
For the same reason we can multiply Eq. (9) by
and therefore it can be absorbed in the normalization constant.
For the same reason we can multiply Eq. (9) by
![$\exp[-\overline{x}^2/(2\sigma_C^2)]$](img102.png) , thus getting,
by complementing the exponential,
, thus getting,
by complementing the exponential,
We can now recognize in it, at first sight,
a Gaussian distribution of the variable 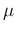 around
around 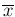 ,
with standard deviation
,
with standard deviation 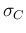 , i.e.
, i.e.
with expected value 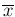 and standard deviation
and standard deviation 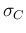 .
.
Someone might be worried about the dependence of the inference on
the flat prior of 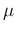 , written explicitly in Eq. (12),
but what really matters is that
, written explicitly in Eq. (12),
but what really matters is that 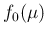 does not vary much
in the region of a few
does not vary much
in the region of a few 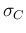 's around
's around 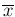 .
Since in the software package that we are going to use, starting
from next section, an explicit prior is required,
let us try to understand
the influence of a vague but not flat prior in the resulting inference.
Let us model
.
Since in the software package that we are going to use, starting
from next section, an explicit prior is required,
let us try to understand
the influence of a vague but not flat prior in the resulting inference.
Let us model 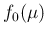 with a Gaussian distribution having a
rather large
with a Gaussian distribution having a
rather large 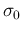 (e.g.
(e.g.
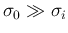 )
and centered in
)
and centered in
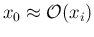 . The result is that
Eq. (7) becomes
. The result is that
Eq. (7) becomes
This is equivalent to add the extra term
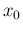 with standard uncertainty
with standard uncertainty 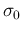 , which
has then to be included in the calculation of
, which
has then to be included in the calculation of 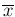 and
and 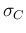
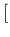 technically the index
technically the index 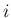 in the sums in
Eqs. (10) and (11)
run from 0 to
in the sums in
Eqs. (10) and (11)
run from 0 to 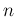 ,
instead than from
,
instead than from 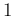 to
to 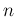 , being
, being 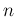 the number of measurements
the number of measurements![$]$](img27.png) .
But if
.
But if
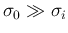 (more precisely
(more precisely
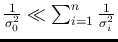 )
and
)
and 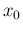 is `reasonable',
then
the extra contribution is irrelevant.
is `reasonable',
then
the extra contribution is irrelevant.
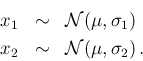
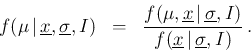
![\begin{eqnarray*}
f(\mu\,\vert\,\underline{x},\underline{\sigma},f_0(\mu)=k) &\...
...\left[- \frac { (\mu-\overline{x})^2}
{2\,\sigma_C^2}
\right]
\end{eqnarray*}](img103.png)
![]() , written explicitly in Eq. (12),
but what really matters is that
, written explicitly in Eq. (12),
but what really matters is that ![]() does not vary much
in the region of a few
does not vary much
in the region of a few ![]() 's around
's around ![]() .
Since in the software package that we are going to use, starting
from next section, an explicit prior is required,
let us try to understand
the influence of a vague but not flat prior in the resulting inference.
Let us model
.
Since in the software package that we are going to use, starting
from next section, an explicit prior is required,
let us try to understand
the influence of a vague but not flat prior in the resulting inference.
Let us model ![]() with a Gaussian distribution having a
rather large
with a Gaussian distribution having a
rather large ![]() (e.g.
(e.g.
![]() )
and centered in
)
and centered in
![]() . The result is that
Eq. (7) becomes
. The result is that
Eq. (7) becomes