- ... occur.1
- Remember
that all events
of our life were indeed VERY improbable, if observed with enough detail,
because they are just points in a high dimensional configuration space!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... uncertainties2
- For the meaning of error
and uncertainty see [1] and [2]. Hereafter
`error' in quote marks is to remind that the noun refers
in reality to uncertainty, or, more precisely,
standard uncertainty.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...tab:masseK_PDG.3
- Details
can be found in the 2000 edition of the PDG [11].
Moreover, comparing the two editions of the PDG and taking
into account that not always the details of the experiment are
publicly available, it is clear that a serious work
to determine at best the charged kaon mass goes beyond the aim of this paper,
being mainly methodological.
Nevertheless,
the uncertainty reported for the 5th result of table
Tab. 1 is not a good account of the
experimental result, as it will be discussed later on in this paper.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... interpretation4
- Note that
this interpretation is valid, under hypotheses which generally
hold, especially if
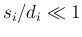 (as it happens in this case),
even if the results were produced with frequentistic methods
that do not contemplate the possibility of attributing
probabilities to the values of physics
quantities. In fact, most results obtained using standard statistics
('frequentistic') are based on the analysis of the so called
likelihood around its maximum. And they can then be easily turned into
probabilistic results
(see e.g. [12], in particular section 12.2.1
and the related figure 12.1).
(as it happens in this case),
even if the results were produced with frequentistic methods
that do not contemplate the possibility of attributing
probabilities to the values of physics
quantities. In fact, most results obtained using standard statistics
('frequentistic') are based on the analysis of the so called
likelihood around its maximum. And they can then be easily turned into
probabilistic results
(see e.g. [12], in particular section 12.2.1
and the related figure 12.1).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...MeV,5
- In most cases
I stick here to two digits for the standard uncertainty.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... indovina”.6
- “To think badly would be to sin,
but very often one gets it right”
 .
Most Italians attribute it to Giulio Andreotti,
but it seems due no less then to a pope [13].
.
Most Italians attribute it to Giulio Andreotti,
but it seems due no less then to a pope [13].
 https://forum.wordreference.com/threads/a-pensare-male-si-fa-peccato-ma-spesso-ci-si-azzecca.2397506/
https://forum.wordreference.com/threads/a-pensare-male-si-fa-peccato-ma-spesso-ci-si-azzecca.2397506/
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 50 keV,7
- Value just decided by eye
looking at the figure with some experienced colleagues, and not resulting
from fits or optimizations of any kind.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... above;8
- A possible alternative would be to allow a shift
of the measured quantity. However this model seems unable to
yield multimodal final pdf's, which is, in my opinion, one of the
desiderata of the model, as stated here.
Perhaps the question requires further study
but, given the limited aims of this paper, I prefer to stick
for the moment to the models of Refs. [15,16].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... interest.9
- For the Gauss' use of what we would
nowadays call a Bayesian reasoning, starting form
the concept of probabilities of the true value, see
Section 6.12 of Ref. [12] based
on Section III of Book II of Ref. [17]
 see Ref. [19] for
details on the missing steps between Eq.(6.53) and Eq.(6.54)
see Ref. [19] for
details on the missing steps between Eq.(6.53) and Eq.(6.54)![$]$](img27.png) .
Here I just want to comment on the meaning of a `flat' prior, which does
not imply
that it has to be interpreted as strictly constant all over the real axis.
With this respect it is interesting the comment that Gauss
adds after he derived the `Gaussian' as the error function
characterized by good mathematical behavior and such that
the posterior gets its maximum in correspondence
of the arithmetic average,
in the case of independent measurements characterized by the same
error probability distribution:
“The function just found
.
Here I just want to comment on the meaning of a `flat' prior, which does
not imply
that it has to be interpreted as strictly constant all over the real axis.
With this respect it is interesting the comment that Gauss
adds after he derived the `Gaussian' as the error function
characterized by good mathematical behavior and such that
the posterior gets its maximum in correspondence
of the arithmetic average,
in the case of independent measurements characterized by the same
error probability distribution:
“The function just found 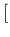 the `Gaussian'
the `Gaussian'![$]$](img27.png) cannot,
it is true, express rigorously the probabilities of the errors: for
since the possible errors are in all cases confined
within certain limits, the probability of errors exceeding those
limits ought always be zero, while our formula always gives some value.
However, this defect, which every analytical function must, from its nature,
labor under, is of no importance in practice, because the value of
function decreases so rapidly, when
cannot,
it is true, express rigorously the probabilities of the errors: for
since the possible errors are in all cases confined
within certain limits, the probability of errors exceeding those
limits ought always be zero, while our formula always gives some value.
However, this defect, which every analytical function must, from its nature,
labor under, is of no importance in practice, because the value of
function decreases so rapidly, when 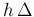
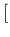 `
`
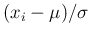 ', in modern notation
', in modern notation![$]$](img27.png) has acquired a considerable magnitude, that it can safely be considered
as vanishing. Besides, the nature of the subject never admits of assigning with
absolute rigor the limits of error.” [18]
has acquired a considerable magnitude, that it can safely be considered
as vanishing. Besides, the nature of the subject never admits of assigning with
absolute rigor the limits of error.” [18]
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... outcomes,10
- In this
introductory section we use
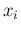 to indicate an individual
observation, while in general the
to indicate an individual
observation, while in general the 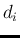 of Tab. 1
are results of `statistical analyses' based
on many direct `observations'.
of Tab. 1
are results of `statistical analyses' based
on many direct `observations'.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... denominator.11
- Let us remind that, in general,
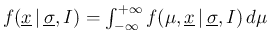 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Sampler,12
- Talking
about the Gibbs sampler algorithm applied in
probabilistic inference (and forecasting) it is impossible
not to to mention the BUGS project [23], the acronym staying
for Bayesian inference using
Gibbs Sampler, that has
been a kind of revolution in Bayesian analysis,
decades ago limited to simple cases because of computational problems
(see also Section 1 of [24]).
In the project web site [25]
it is possible to find packages with excellent Graphical User Interface,
tutorials and many examples [26], which, although
far from the typical interests of physicists,
might help to understand the underlying reasoning
and the model language, practically the same used by JAGS.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... case,13
- But in frontier research it is not difficult
to imagine cases in which this is not true.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... interest.14
- My preferred vademecum of Probability
Distributions is the homonymous app [30].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
positive.15
- Also a mass, as many other physics quantities,
is positively defined, and in principle one has to
pay attention,
either in the sampling steps or when the resulting chain
is analyzed,
that it does not get negative
But this problem does not occur in practice if the
the average value
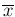 is many standard
is many standard 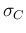 above zero. Anyway, packages like JAGS allow
also sharp constrains on the priors.
(This is general problem when we use Gaussians to describe
positively defined quantities, already realized by Gauss
and reminded in footnote 9.)
above zero. Anyway, packages like JAGS allow
also sharp constrains on the priors.
(This is general problem when we use Gaussians to describe
positively defined quantities, already realized by Gauss
and reminded in footnote 9.)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... script16
- If these
lines are saved
in a file, e.g. kaon_mass_naive.R,
then the script can be run with the command
source('kaon_mass_naive.R').
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...list17
- A `list' is a very
interesting object of R, which can contain other objects, also
of different kinds and different lengths; the element of a `list'
can be accessed either by name, as we do here, or by indices.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...sceptical1999,18
- For easier
comparison
with the results of Ref. [15]
for the Gamma parameters we use hereafter
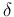 and
and 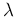 instead of the standard
instead of the standard 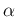 and
and 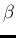 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... average.19
- An example in which the sceptical
combination produces a result narrower that the
weighted average is shown in the Appendix.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... figure,20
- The histogram with the over-imposed profile was produced
by
chain.df <- as.data.frame( as.mcmc(chain) )
hist(chain.df$mu,nc=100,prob=TRUE,xlab='K mass (MeV)',ylab='f(m)', col='cyan',main=”)
lines(density(chain.df$mu, adjust=1.0), lwd=3)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... required.21
- Presently the
value of the charged kaon mass, with relative
uncertainty of around 26 ppm, is not critical for
fundamental issues.
For example its contribution
to
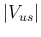 of the Standard Model is of the order of 66 ppm,
to be combined
in quadrature with the relative uncertainties of the other quantities
from which
of the Standard Model is of the order of 66 ppm,
to be combined
in quadrature with the relative uncertainties of the other quantities
from which 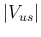 depends (the branching ratios of interest
depend on
depends (the branching ratios of interest
depend on
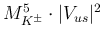 and hence the relative uncertainty
on
and hence the relative uncertainty
on 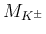 is propagated with a factor
is propagated with a factor 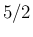 into the
relative uncertainty on
into the
relative uncertainty on 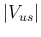 ).
).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... freedom,22
- Providing just `
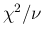 '
is, as now well understood, rather misleading, because
the
'
is, as now well understood, rather misleading, because
the 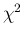 does not scale with
does not scale with 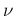 . Therefore, though a ratio of 2.31
would be a clear alarm bell for
. Therefore, though a ratio of 2.31
would be a clear alarm bell for 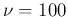 , it is quite `in the norm'
for
, it is quite `in the norm'
for 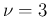 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
rounding23
- Indeed, if we just calculate weighted
averages and related standard deviations, with no
arbitrary scaling, the result does not change if we use
the individual results or we group them in steps.
This is related to the important concept of `statistical
sufficiency', that will be treated in detail, for the Gaussian case,
in the forthcoming Ref. [35].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... parameters:24
- Someone would be surprised
about the possibility of inferring a number of parameters
superior to the number of the data points. This is not really
a conceptual problem, as long as we understand that
they are correlated, often in a complicate way and of which
the correlation matrix is just a first order representation
(and we have to be careful when using it in further
analyses [36]).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... matrix:25
- Technical remark:
the correlation matrix has been obtained by the R function cor(),
applied
to the chain after a suitable transformation.
For example, one can transform it into a data frame and then
apply cor() to it:
> chain.df <- as.data.frame( as.mcmc(chain) )
> round(cor(chain.df),2)
that includes the rounding at two decimal digits (' ' is the R prompt).
' is the R prompt).
Or, more simply, we can convert the chain into a matrix,
each column containing the occurrences of each variable during the sample,
and calculate then the correlations between them. This is
how to do it in short, with nested calls to functions
(remember also print(), if the command hat to be included into a script):
> round(cor(as.matrix(chain)),2)
And here are some useful commands to understand what is going on:
> chain.M <- as.matrix(chain)
> str(chain.M)
> dimnames(chain.M)
> mean(chain.M[,"mu"])
> mean(chain.M[,1])
> mean(chain.M[,"r[9]"])
> mean(chain.M[,10])
> cor(chain.M[,"mu"], chain.M[,"r[9]"])
> cor(chain.M[,1], chain.M[,10])
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... `statistical'26
- For example
it is important
to understand how the
`errors' were evaluated, also because we are aware of the old custom
(maintained also presently by several experimental teams)
of using for `systematic errors' extreme variations
for sake of safety, thus providing very conservative `error',
instead than standard uncertainties [1,2].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.