It is not rare the case in which experimental
results `appear' to be in mutual disagreement. The quote marks
are mandatory, as a reminder that
also very improbable events might by nature occur.1The fact that they `appear' to us
in mutual disagreement is because we know by
experience that uncertainties2might be underestimated,
systematic errors overlooked, theoretical corrections not (properly)
taken into account,
or even mistakes of
different kinds having possibly
been made in building/running the experiment or in the
data handling.
It is enough to browse the PDG [3] to find
cases of this kind, as the one of Fig. 1
concerning the mass of the charged kaon, whose values,
as selected by the PDG,
Figure:
Charged kaon mass from several experiments
as summarized by the PDG [3]. Note that besides
the `error' of 0.013 MeV, obtained by a 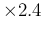 scaling,
also an `error' of 0.016 MeV is provided,
obtained by a
scaling,
also an `error' of 0.016 MeV is provided,
obtained by a 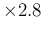 scaling. The two results are
called `OUR AVERAGE' and 'OUR FIT', respectively.
scaling. The two results are
called `OUR AVERAGE' and 'OUR FIT', respectively.
 |
are reported in Tab. 1.3
Table:
Experimental values of the charged kaon mass,
limited to those taken into account
by the 2019 issue of PDG [3] (see footnote 3
for remarks).
| |
Authors |
pub. year |
central value ![$[d_i]$](img17.png) |
uncertainty ![$[s_i]$](img18.png) |
|
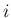 |
|
|
(MeV) |
(MeV) |
|
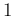 |
G. Backenstoss et al. [4] |
1973 |
493.691 |
0.040 |
|
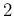 |
S.C. Cheng et al. [5] |
1975 |
493.657 |
0.020 |
|
 |
L.M. Barkov et al.[6] |
1979 |
493.670 |
0.029 |
|
 |
G.K. Lum et al. [7] |
1981 |
493.640 |
0.054 |
|
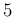 |
K.P. Gall et al. [8] |
1988 |
493.636 |
0.011 (*) |
|
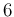 |
A.S. Denisov et al. [9] |
1991 |
493.696 |
 0.0059 0.0059![$]$](img27.png) |
|
| |
& Yu.M. Ivanov [10] |
1992 |
 same same![$]$](img27.png) |
0.007 |
|
|
The usual probabilistic interpretation4of the results is that each experiment
provides a probability density function (pdf) centered in 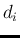 with standard deviation
with standard deviation 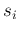 , as shown by the solid lines
of Fig. 2.
, as shown by the solid lines
of Fig. 2.
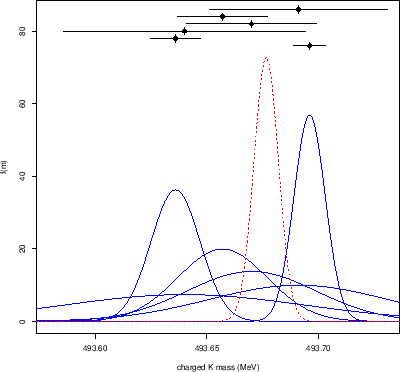
Figure:
Graphical representation of the results on the charged kaon mass
of Tab. 1 (solid lines). The dashed red Gaussian shows the result
of the naive standard combination (see text).
 |
The standard way to combine the individual results consists in
calculating the weighted average, with weights equal to 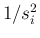 , that is
, that is
which, applied to the values of Tab. 1,
yields
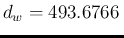 MeV and
MeV and
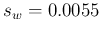 MeV, i.e.
a charged kaon mass of
MeV, i.e.
a charged kaon mass of
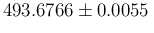 MeV,5 graphically
shown in Fig. 2 with a dashed red Gaussian.
The outcome `appears' suspicious because the probability mass is concentrated
in the region less preferred by the individual more precise results,
as also emphasized in the ideogram of Fig. 1,
on the meaning of which we shall return in section 5.
MeV,5 graphically
shown in Fig. 2 with a dashed red Gaussian.
The outcome `appears' suspicious because the probability mass is concentrated
in the region less preferred by the individual more precise results,
as also emphasized in the ideogram of Fig. 1,
on the meaning of which we shall return in section 5.
As a matter of fact, a situation of this kind is not impossible, but
nevertheless, there is a natural tendency to believe that
there must be something not properly taken into account by one or more
experiments. Told with a dictum attributed to a famous Italian politician,
“a pensar male degli altri si fa peccato ma spesso ci si
indovina”.6
Figure:
Same as Fig. 2 but with one
result arbitrarily shifted by 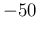 keV (dotted line).
keV (dotted line).
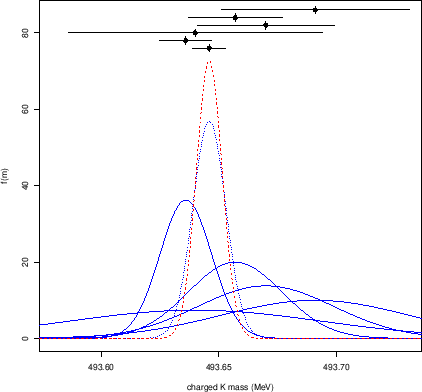 |
For example, looking at Fig. 2, one is
strongly tempted to
lower, just as an exercise, the highest value
by 50 keV,7thus getting the excellent overall agreement shown in
Fig. 3
(shifted Gaussian plotted with a dotted gray line),
yielding a combined mass value of
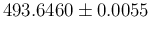 MeV.
And the question would be settled. But this sounds at least
unfair.
In particular because we are aware, from the history of measurements,
of a kind of `inertia' of new results to different from old
ones
- but sometimes the new results moved `too far' from the
old ones and the presently accepted value
lies somewhere in the middle.
MeV.
And the question would be settled. But this sounds at least
unfair.
In particular because we are aware, from the history of measurements,
of a kind of `inertia' of new results to different from old
ones
- but sometimes the new results moved `too far' from the
old ones and the presently accepted value
lies somewhere in the middle.
Figure:
Some history plots from the
PDG [3,14].
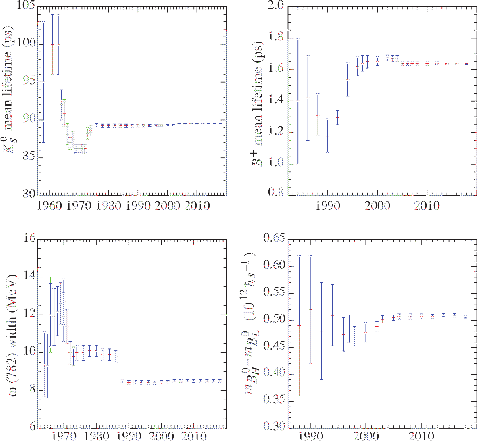 |
Figure 4 shows some of the history plots
traditionally reported by the PDG [14].
In such a state of uncertainty, probability theory can help us
in building up a model in which the values about which we are in doubt
are allowed to vary from the nominal ones. Obviously, the model is not
unique, as not unique are the probability distributions that can be used.
Following then [15], inspired to [16], these
are the criteria followed and some (hopefully shareable)
desiderata:
- the quantities on which we focus our doubts are
the reported uncertainties
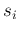 , assumed to have the meaning of
standard uncertainty [1,2], as commented
above;8
, assumed to have the meaning of
standard uncertainty [1,2], as commented
above;8
- the `true' standard deviations
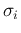 are related
to
are related
to 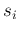 by a factor
by a factor 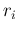 (one for each experiment), i.e.
(one for each experiment), i.e.
where the last notation means that 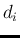 is described
by a Gaussian (`normal') distribution centered on the `true'
value of the quantity of interest, generically indicated by
is described
by a Gaussian (`normal') distribution centered on the `true'
value of the quantity of interest, generically indicated by 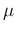 ,
with standard deviation
,
with standard deviation 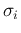 ;
;
- all experiments are treated democratically and fairly, i.e. our prior belief of each
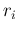 has expected value equal to 1, and its prior distribution
does not depend on the experiment:
has expected value equal to 1, and its prior distribution
does not depend on the experiment:
where `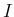 ' stands for the background status of information
(probability is always conditional probability!);
' stands for the background status of information
(probability is always conditional probability!);
- but we are sceptical, and hence each
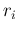 has à priori
a wide range of possibilities
described by a suitable (easy to handle) probability distribution,
the details of which will be give later - we just anticipate that
we take a prior 100% standard uncertainty on
has à priori
a wide range of possibilities
described by a suitable (easy to handle) probability distribution,
the details of which will be give later - we just anticipate that
we take a prior 100% standard uncertainty on 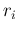 ,
i.e.
,
i.e.
![$\sigma(r_i\,\vert\,I)/\mbox{E}[r_i\,\vert\,I]=1$](img51.png) ;
;
- one of the desiderata of the model is that the posterior pdf
of the physical quantity of interest
should not be limited to a Gaussian and could even be multimodal
if the individual results cluster in different regions;
or it could be narrower than the pdf obtained by the
standard weighted average, if the individual results tend to overlap
`too much'
(see e.g. Figs. 4 and 5 of
Ref. [15]);
- finally, once the parameters of
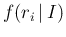 are defined on bench marks and checked against `reasonable'
variation (as done in Figs. 4 and 5 of
Ref. [15]), fine tuning and cherry peaking
of the individual results to be included in the
combination should be avoided (unless we have good reasons
to mistrust some results).
are defined on bench marks and checked against `reasonable'
variation (as done in Figs. 4 and 5 of
Ref. [15]), fine tuning and cherry peaking
of the individual results to be included in the
combination should be avoided (unless we have good reasons
to mistrust some results).
Once the model has been built, we can easily write down
the multidimensional
probability pdf
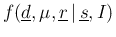 ,
of all the variables of interest
(the `observed'
,
of all the variables of interest
(the `observed' 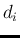 and
the uncertain values
and
the uncertain values 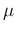 and
and 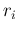 's - the
's - the 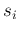 will
be instead considered as fixed conditions, as it will be clear in a while;
will
be instead considered as fixed conditions, as it will be clear in a while;
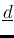 stands for all the
stands for all the 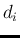 , and so on).
, and so on).
Once the multi-dimensional pdf has been
settled, writing down the unnormalized
pdf of the uncertain quantities,
is straightforward, as we shall see in a while. But, differently from
[15], the rest of the technical work (normalization,
marginalization and calculation of the moments of interest) will
be done here by sampling, i.e. by Monte Carlo, and the use of a
suitable software package will make the task rather easy.
But, before we build up the model of interest, let us start
with a simpler one, in which
we fully trust the reported standard uncertainty, i.e.
we assume
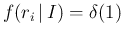 , and hence
, and hence 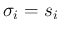 .
We also take for the prior,
following Gauss [17,18],
a flat distribution of
.
We also take for the prior,
following Gauss [17,18],
a flat distribution of 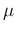 in the region of interest.9
in the region of interest.9

![]() with standard deviation
with standard deviation ![]() , as shown by the solid lines
of Fig. 2.
, as shown by the solid lines
of Fig. 2.

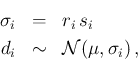
![\begin{eqnarray*}
f(r_1\,\vert\,I) &=& f(r_2\,\vert\,I)\ = \ f(r_3\,\vert\,I)\ =\ \cdots \\
\mbox{E}[r_i\,\vert\,I] &=& 1\,,
\end{eqnarray*}](img49.png)
![]() , and hence
, and hence ![]() .
We also take for the prior,
following Gauss [17,18],
a flat distribution of
.
We also take for the prior,
following Gauss [17,18],
a flat distribution of ![]() in the region of interest.9
in the region of interest.9