Sceptical combination with JAGS - Results

The core of the R script is very similar to the one of section 3.2, besides the model used, the number of iterations and the variables to be monitored. Note that we pass the Gamma parameter delta and lambda to the model via the list data (a different choice could have been to define them directly inside the model). Here is the entire script, including statistics and plot summaries (plots not shown here).

library(rjags)
data <- NULL             # 'data' to be passed to the model
data$d  <- c(493.691, 493.657, 493.670, 493.640, 493.636, 493.696)
data$s  <- c(  0.040,   0.020,   0.029,   0.054,   0.007,   0.007)
data$N  <- length(data$d)
data$delta  = 1.3   #  parameters of Gamma(omega):  delta  <--> 'alpha'  
data$lambda = 0.6   #                               lambda <--> 'beta'

jm <- jags.model(model, data)                            # define the model
update(jm, 1000)                                         # burn in 
chain <- coda.samples(jm, c("mu", "r"), n.iter=100000)   # sampling 

print(summary(chain))
plot(chain)

This is what we get from summary(chain):

1. Empirical mean and standard deviation for each variable,
   plus standard error of the mean:

         Mean      SD  Naive SE Time-series SE
mu   493.6678 0.01608 1.608e-05      0.0000515
r[1]   0.8790 0.53138 5.314e-04      0.0006477
r[2]   0.9671 0.63559 6.356e-04      0.0010050
r[3]   0.8330 0.49631 4.963e-04      0.0005264
r[4]   0.8450 0.50271 5.027e-04      0.0005771
r[5]   2.1528 1.62050 1.621e-03      0.0034153
r[6]   2.9148 2.35537 2.355e-03      0.0052502

2. Quantiles for each variable:

         2.5%      25%      50%      75%   97.5%
mu   493.6394 493.6555 493.6666 493.6807 493.696
r[1]   0.3763   0.5713   0.7457   1.0179   2.177
r[2]   0.3803   0.5965   0.8054   1.1338   2.515
r[3]   0.3656   0.5467   0.7090   0.9619   2.045
r[4]   0.3703   0.5550   0.7194   0.9753   2.077
r[5]   0.5391   1.1500   1.7672   2.6621   6.101
r[6]   0.5073   1.3988   2.4184   3.7211   8.600

The result is then a mass of $493.668\pm 0.016\,$MeV, where the `error' is provided by the standard uncertainty [1,2]. However, this does not imply that the value of the mass is normally distributed around the average.<sup>19</sup>This can be checked on the quantiles of `mu' (see above output), and better on the histogram of the sampled values, shown in the upper plot of Fig. 10,

Figure: Above: histogram of charged kaon mass by MCMC sampling. Below: profile of the above histogram compared with the individual results, the naive weighted average (dashed) and the Gaussian based on the average and the PDG prescription to scale the `error' (see text).

whose smoothed profile is reported in the bottom plot of the same figure,²⁰together with the individual measurements, the standard weighted average (red dashed) and the combination got following the PDG prescriptions (gray) with the $\times 2.4$ (narrower curve) and $\times 2.8$ scaling (wider curve) [3].

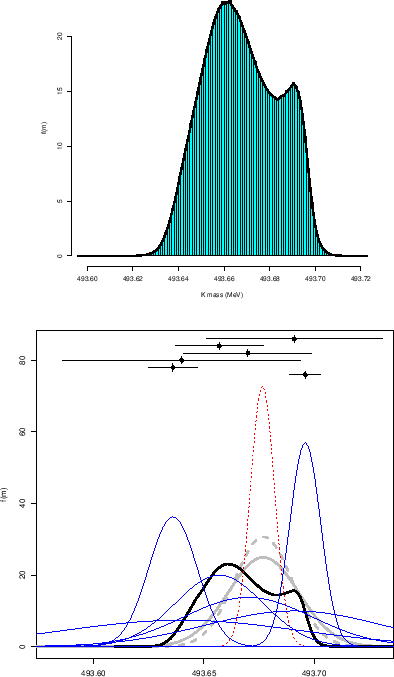Here is a summary of the results:

method		$m_{K^{\pm}}$ (MeV)
simple weighted average		$493.677 \pm 0.006$
PDG (`OUR AVERAGE', $\times 2.4$ scaling)		$493.677 \pm 0.013$
PDG (`OUR FIT', $\times 2.8$ scaling)		$493.677\pm 0.016$
sceptical		$493.668\pm 0.016\,$

As far as the rescaling factor $r_i$ are concerned, we see from the output of the summary that only those relative to the items 5 and the 6 are preferred to be higher the the initial ones, with mean values 2.2 and 2.9, respectively. Therefore with this data set the most 'suspicious' one is nr. 6, as we had judged by eye in the introduction. But since the $r_i$ were inferred simultaneously, and together with the mass, it is interested to give a look to the correlation matrix. Here is directly the R output:

        mu  r[1]  r[2]  r[3]  r[4]  r[5]  r[6]
mu    1.00 -0.21  0.31 -0.03  0.16  0.55 -0.59
r[1] -0.21  1.00 -0.05  0.02 -0.03 -0.11  0.13
r[2]  0.31 -0.05  1.00  0.03  0.06  0.18 -0.17
r[3] -0.03  0.02  0.03  1.00  0.00 -0.01  0.02
r[4]  0.16 -0.03  0.06  0.00  1.00  0.09 -0.09
r[5]  0.55 -0.11  0.18 -0.01  0.09  1.00 -0.32
r[6] -0.59  0.13 -0.17  0.02 -0.09 -0.32  1.00

We see, for example, that the highest correlation of the mass (`mu') is with r[5] and r[6], related to the two most precise measurements: the first is positive, meaning that a larger $\sigma_5$ would allow mu to rise towards $d_6$; the second is negative, meaning that a larger $\sigma_6$ would allow mu to descend towards $d_5$. For this reason, among the several $r_i$, r[5] and r[6] get the highest (in absolute value) correlation coefficient, having a negative sign. But it is only $-32\%$, indicating that $\sigma_5$ and $\sigma_6$ could possibly be both larger than the stated standard uncertainty.

Going back to the mass value, we see that our result does not differ much from the PDG one, if we are only interested in average and standard uncertainty (just $-9\,$keV lower, with similar uncertainty). What differs mostly is the shape of the probability distribution, which is has nothing to do with a Gaussian. Instead, in the the weighted average, with the resulting `error' as it comes straight from Eq. (2) or scaled with $\sqrt {\chi ^2/\nu }$, the interpretation is tacitly Gaussian, or it is assumed as such in further analyses [35]. For example, if one is interested, for some deep physical reasons, in the chance that the mass is larger than 493.70 MeV, it is clear from the bottom plot of Fig. 10 that the results would be quite different.

One might argue if, for such a purpose, we could use the bi-modal curve of the PDG ideogram (see Fig. 1), in alternative to the pdf resulting from the sceptical analysis performed here. But what is the meaning of the bi-modal curve of Fig. 1? If one compares it with the individual Gaussians reported in Fig. 2 we see that it follows somehow the profile of highest points of the curves. Therefore the first guess is that it is just an unnormalized sum, that is $\sum_if_{\cal N}(m\,\vert\,d_i,\sigma_i)$. But checking it, it does not seem to be the case. The second guess was a kind of weighted average, with weights equal to $1/s_i^2$, i.e. $\sum_if_{\cal N}(m\,\vert\,d_i,\sigma_i)/s_i^2$, but it did not work either. The third attempt was to set the weights to $1/s_i$, i.e. $\sum_if_{\cal N}(m\,\vert\,d_i,\sigma_i)/s_i$, and this seems to be the case. The three attempts are reported in Fig. 11, but just as a curiosity, as they have no probabilistic meaning.

Figure: Attempts to re-obtain the bi-modal curve shown in the PDG ideogram of Fig. 1. They are not normalized but just equalized to the value of their maximum. Solid line: $\propto \sum _i f_{\cal N}(m\,\vert\,d_i,s_i)/s_i$; dotted line: $\propto \sum _i f_{\cal N}(m\,\vert\,d_i,s_i)$; dashed line: $\propto \sum _i f_{\cal N}(m\,\vert\,d_i,s_i)/s_i^2$.

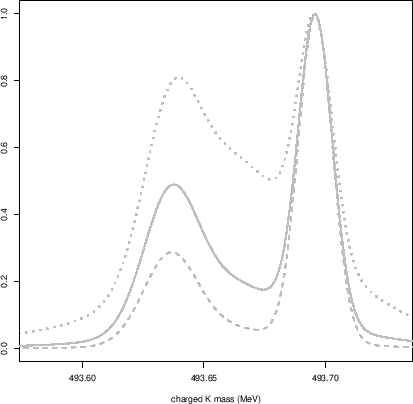Let us end this section showing how to re-obtain the standard combination with the same general model used in the sceptical combination. We just need to choose values suitable $\delta$ and $\lambda$ to get $\mbox{E}[r_i]=1$ and $\sigma(r_i)\rightarrow 0$. Inverting Eqs. (13) and (14) of [15] seems complicate, but in the limit of zero variance, this is the same as requiring $\mbox{E}[\omega_i]=1$ and $\sigma(\omega_i)\rightarrow 0$, a condition easier to apply in practice. Being in fact $\mbox{E}[\omega_i]=\delta/\lambda$ and $\mbox{var}[\omega_i]=\delta/\lambda^2 = (\delta/\lambda)/\lambda$, the requirement simply translates into $\delta=\lambda$ with both parameters `very large'. In practice is is enough to set e.g. $\delta=\lambda=10000$ to recover the result of the weighed average of $493.6766\pm 0.0055\,$MeV.