


Next: Falsificationism and its statistical
Up: From Observations to Hypotheses
Previous: From Observations to Hypotheses
Figure 1:
From observations to hypotheses.  The link
between value of a quantity and theory is a reminder
that sometimes a quantity has meaning only
within a given theory or model [1].
The link
between value of a quantity and theory is a reminder
that sometimes a quantity has meaning only
within a given theory or model [1].
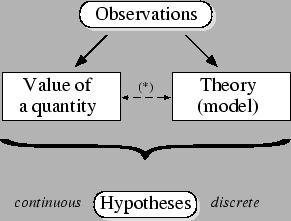 |
The intellectual process of learning from observations can be
sketched as illustrated in figure 1.
From experimental data we wish to `determine' the value of
some physical quantities,
or to establish which theory describes `at best'
the observed phenomena. Although these two
tasks are usually
seen as separate issues, and analyzed with different
mathematical tools, they
can be viewed as two subclasses of the same process:
inferring hypotheses from observations.
What differs between the two kinds of inference
is the number of hypotheses that enters the game:
a discrete, usually small number when dealing with
theory comparison;
a large, virtually infinite number
when inferring the value of physical quantities.
In general, given some data (past observations),
we wish to:
- select a theory and determine its parameters
with the aim to describe and `understand' the physical world;
- predict future observations (that, once they are recorded,
they join the set of past observations to corroborate or diminish
our confidence on each theory and its parameters).
The process of learning from data and predicting new
observations is characterized by uncertainty
(see figure 2).
Figure 2:
Theory (and the
value of its parameters) acting as a link between
past and future.
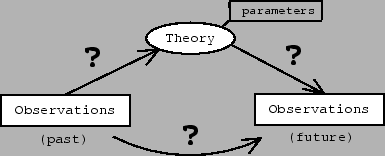 |
Uncertainty in
going from past observations to the theory and its parameters.
Uncertainty in predicting precise observations from the theory.
And, as a consequence, uncertainty in predicting
future observations
from past observations.
Rephrasing the
hypothesis-observation scheme
in terms of causes and effects,
we can realize that
the very source of uncertainty is
due to the not biunivocal relationship between causes and effects,
as sketched in figure
3.
The fact that identical causes
-- identical according to our knowledge
-- might produce different effects can be due to
internal (intrinsic) probabilistic aspects of the theory, as well as to
our lack of knowledge about the exact set of
causes.1(Experimental errors are one of the components of the external
probabilistic behavior of the observations.)
However, there is no practical difference between the two situations,
as far as
the probabilistic behavior of the result is concerned
(i.e. in the status of our mind concerning the possible outcomes of the experiment),
and hence to the probabilistic character of inference.
Figure 3:
Causal links (top-down) and inferential links (down-up).
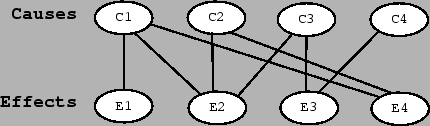 |
Given this cause-effect scheme,
having observed an effect, we cannot be sure about its cause.
(This is what
happens to effects 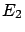 ,
, 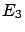 and
and 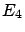 of figure 3 --
effect
of figure 3 --
effect 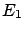 , that can only be
due to cause
, that can only be
due to cause 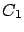 ,
has to be considered an exception, at least in the inferential problems
scientists typically meet.)
,
has to be considered an exception, at least in the inferential problems
scientists typically meet.)
- Example 1.
- As a simple example, think about the effect
identified by the number
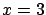 resulting by one of the following random generators
chosen at random:
resulting by one of the following random generators
chosen at random:
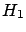 = ``a Gaussian generator with
= ``a Gaussian generator with 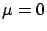 and
and 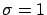 '';
'';
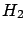 = ``a Gaussian generator with
= ``a Gaussian generator with 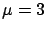 and
and 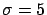 '';
'';
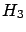 = ``an exponential generator with
= ``an exponential generator with 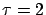 ''
(
''
(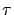 stands for the expected value of the exponential distribution;
stands for the expected value of the exponential distribution;
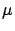 and
and 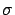 are the usual parameters of the Gaussian distribution).
Our problem, stated in intuitive terms, is to find out which
hypothesis might have caused
are the usual parameters of the Gaussian distribution).
Our problem, stated in intuitive terms, is to find out which
hypothesis might have caused 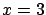 :
: 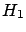 ,
,
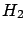 or
or 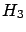 ? Note that none of the hypotheses of this example
can be excluded and, therefore,
there is no way to reach a boolean conclusion. We can
only state, somehow, our rational preferences, based
on the experimental result and
our best knowledge of the behavior of each model.
? Note that none of the hypotheses of this example
can be excluded and, therefore,
there is no way to reach a boolean conclusion. We can
only state, somehow, our rational preferences, based
on the experimental result and
our best knowledge of the behavior of each model.
The human mind is used to live -- and survive --
in conditions of
uncertainty and has developed mental categories to handle it.
Therefore,
although we are in a constant status of uncertainty
about many events which might or might not occur,
we can be ``more or less sure -- or confident --
on something than on something else''.
In other words,
``we consider something more or less probable
(or likely)'', or
``we believe something more or less than
something else''. We can use similar expressions,
all referring to the intuitive idea of probability.
The status of uncertainty
does not prevent us from
doing Science. Indeed, said with Feynman's words,
``it is scientific
only to say what is more likely and what is less
likely''[3].
Therefore, it becomes crucial to
learn how to deal quantitatively with probabilities of causes,
because the ``problem(s) in the probability of causes ...
may be said to be the essential problem(s) of
the experimental method'' (Poincaré[4]).
However, and unfortunately, it is a matter of fact that
nowadays most scientists are
incapable to reason correctly about probabilities of causes,
probabilities of hypotheses, probabilities
of values of a quantities,
and so on. This lack of expertise is due to
the fact that we have been educated and trained
with a statistical theory in which the very concept of probability
of hypotheses is absent, although we naturally tend to think and
express ourselves in such terms. In other words, the common prejudice
is that probability is the long-term relative frequency,
but, on the other hand, probabilistic statements about hypotheses
(or statements implying,
anyway, a probabilistic meaning) are constantly made by
the same persons, statements that are
irreconcilable with their definition of
probability [5].
The result of this
mismatch between natural thinking and cultural
over-structure produces mistakes in scientific judgment,
as discussed e.g. in Refs. [1,5].
Another prejudice, rather common among scientists, is that, when they
deal with hypotheses, `they think they reason' according to the
falsificationist scheme: hence, the hypotheses tests of conventional
statistics are approached with a genuine intent of proving/falsifying
something. For this reason we need to shortly review these concepts,
in order to show the reasons why they are less satisfactory than
we might naïvely think. (The reader is assumed to be familiar with
the concepts of hypothesis tests, though at an elementary level
-- null hypothesis, one and two tail tests,
acceptance/rejection, significance, type 1 and type 2 errors, an so on.)



Next: Falsificationism and its statistical
Up: From Observations to Hypotheses
Previous: From Observations to Hypotheses
Giulio D'Agostini
2004-12-22


![]() ,
, ![]() and
and ![]() of figure 3 --
effect
of figure 3 --
effect ![]() , that can only be
due to cause
, that can only be
due to cause ![]() ,
has to be considered an exception, at least in the inferential problems
scientists typically meet.)
,
has to be considered an exception, at least in the inferential problems
scientists typically meet.)