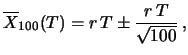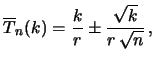Next: Numero di teste meno
Up: Previsioni basate sul teorema
Previous: pzd100Limite a normale della
Indice
Una delle consequenze
del teorema del limite centrale più importanti per le
applicazioni di laboratorio è la distribuzione di probabilità
della media aritmetica. Se si hanno  variabili
casuali indipendenti
variabili
casuali indipendenti 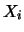 descritte dalla stessa distribuzione
avente valore atteso
descritte dalla stessa distribuzione
avente valore atteso 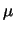 e deviazione standard
e deviazione standard 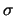 ,
la media aritmetica
,
la media aritmetica
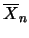 , con
, con  ``sufficientemente grande'',
segue una distribuzione normale di media
``sufficientemente grande'',
segue una distribuzione normale di media 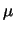 e deviazione standard
e deviazione standard
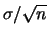 :
Come esempio, possiamo fare delle previsioni
relative al processo di Poisson che abbiamo analizzato a lungo,
di intensità
:
Come esempio, possiamo fare delle previsioni
relative al processo di Poisson che abbiamo analizzato a lungo,
di intensità 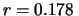 conteggi/s. Considerando le medie
su 100 misure di conteggi di durata 3, 6, 12, 30 e 100 s,
abbiamo:
ovvero:
conteggi/s. Considerando le medie
su 100 misure di conteggi di durata 3, 6, 12, 30 e 100 s,
abbiamo:
ovvero:
Per un confronto con un esperimento simulato si veda la
tabella 5.4.
Consideriamo inoltre le medie dei tempi di attesa per
osservare 1, 2, 5, 10, 20, 50 e 100 eventi:
ove facciamo il caso di 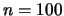 per
per  e
e  per
le altre misure. Otteniamo quindi:
per
le altre misure. Otteniamo quindi:
Si lascia come esercizio il confronto con i risultati
simulati di tabella 1.2.
Qualcuno avrà notato come
le medie dei tempi di attesa di tabella
5.4 sono in ``spettacolare'' accordo con le previsioni.
In effetti esse non erano state effettuate su 100 o 50 misure bensì
su 10000 (vedi figura 4.3). Infatti in questo
caso le previsioni sarebbero state:
Questo spiega la ``quasi perfetta'' corrispondenza fra previsioni e
risultati dei tempi di attesa di tabella 5.4,
che sarebbero stati invece ``sospetti'' nel caso di 50 o 100 misure.




Next: Numero di teste meno
Up: Previsioni basate sul teorema
Previous: pzd100Limite a normale della
Indice
Giulio D'Agostini
2001-04-02