



Next: Incertezze relative
Up: Propagazione delle incertezze
Previous: Caso di combinazioni lineari
Indice
Dalla (11.3)
si ottiene la regola generale per una funzione qualsiasi,
mediante linearizzazione intorno ai valori attesi. Infatti se
indichiamo con 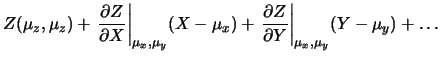 la generica funzione delle due variabili
casuali
la generica funzione delle due variabili
casuali 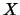 e
e 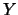 , abbiamo
, abbiamo
dove 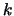 contiene tutti i termini che non dipendono
dalle variabili casuali e che quindi
sono ininfluenti ai fini del calcolo della
varianza. L'ultimo passaggio è stato ottenuto
facendo uso della (11.3).
È generalmente sottointeso
che le derivate vadano calcolate nel punto di migliore stima di
contiene tutti i termini che non dipendono
dalle variabili casuali e che quindi
sono ininfluenti ai fini del calcolo della
varianza. L'ultimo passaggio è stato ottenuto
facendo uso della (11.3).
È generalmente sottointeso
che le derivate vadano calcolate nel punto di migliore stima di 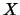 e
di
e
di 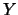 .
Il caso generale va da sé.
.
Il caso generale va da sé.
Si ricordi che la (11.4) è basata su una linearizzazione.
La funzione deve essere abbastanza lineare un certo numero
di deviazioni standard intorno alle migliori stime delle
variabili di partenza.
Questo è generalmente vero
se le 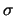 sono molto minori delle stime. Se la funzione è lineare
non c'è nessun vincolo sul valore di
sono molto minori delle stime. Se la funzione è lineare
non c'è nessun vincolo sul valore di 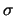 . Ad esempio,
se
. Ad esempio,
se 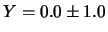 , con
, con
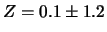 e
e
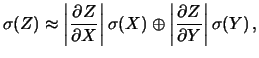 , si ha
, si ha
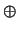 .
.
Per quanto riguarda l'uso della formula di propagazione,
si raccomanda di fare una lista dei
contributi all'incertezza
totale dovuti a ciascun termine da cui la grandezza finale
dipende. Questo permette di capire quale contributo sia
maggiormente
responsabile e sul quale bisogna intervenire al momento di
pianificare un nuovo esperimento. Quindi la formula
(11.4) può essere riscritta nel seguente modo,
didatticamente più valido:
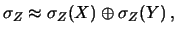 |
(11.5) |
ove con ``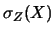 '' si è indicata l'operazione
di somma in quadratura.
C'è un altro modo interessante di riscrivere questa formula:
'' si è indicata l'operazione
di somma in quadratura.
C'è un altro modo interessante di riscrivere questa formula:
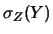 |
(11.6) |
in cui
 e
e
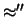 indicano i contribuiti
all'incertezza dovuti a ciascuna delle grandezze da cui
indicano i contribuiti
all'incertezza dovuti a ciascuna delle grandezze da cui 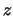 dipende. È infatti istruttivo abituarsi a pensare in termini
delle componenti all'incertezza totale, piuttosto che usare
ciecamente la formula (11.4).
È inoltre importante
dare alle derivate il significato
di coefficiente di sensibilità, nel senso che,
maggiore è la derivata, maggiore è la variazione di
dipende. È infatti istruttivo abituarsi a pensare in termini
delle componenti all'incertezza totale, piuttosto che usare
ciecamente la formula (11.4).
È inoltre importante
dare alle derivate il significato
di coefficiente di sensibilità, nel senso che,
maggiore è la derivata, maggiore è la variazione di 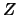 a parità di variazione di
a parità di variazione di 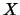 o di
o di 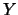 .
.
Naturalmente le (11.4)-11.6 si
generalizzano facilmente al caso di molte variabili. Inoltre, d'ora
in poi useremo il simbolo ``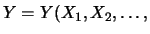 '' invece di ``
'' invece di ``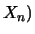 ,
anche se bisogna tenere ben in mente che si tratta sempre di
formule approssimate, a meno che la funzione non sia lineare,
ovvero la grandezza finale è combinazione
lineare di quelle iniziali.
,
anche se bisogna tenere ben in mente che si tratta sempre di
formule approssimate, a meno che la funzione non sia lineare,
ovvero la grandezza finale è combinazione
lineare di quelle iniziali.




Next: Incertezze relative
Up: Propagazione delle incertezze
Previous: Caso di combinazioni lineari
Indice
Giulio D'Agostini
2001-04-02
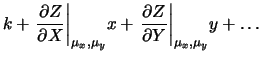
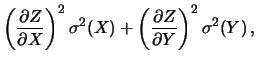
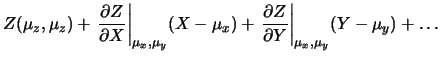 la generica funzione delle due variabili
casuali
la generica funzione delle due variabili
casuali ![]() sono molto minori delle stime. Se la funzione è lineare
non c'è nessun vincolo sul valore di
sono molto minori delle stime. Se la funzione è lineare
non c'è nessun vincolo sul valore di ![]() . Ad esempio,
se
. Ad esempio,
se ![]() , con
, con
![]() e
e
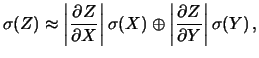 , si ha
, si ha
![]() .
.
![]() '' invece di ``
'' invece di ``![]() ,
anche se bisogna tenere ben in mente che si tratta sempre di
formule approssimate, a meno che la funzione non sia lineare,
ovvero la grandezza finale è combinazione
lineare di quelle iniziali.
,
anche se bisogna tenere ben in mente che si tratta sempre di
formule approssimate, a meno che la funzione non sia lineare,
ovvero la grandezza finale è combinazione
lineare di quelle iniziali.