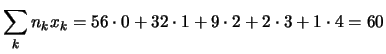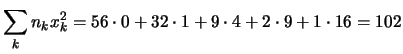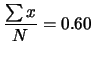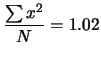Next: Effetto del raggruppamento in
Up: Descrizione quantitativa dei dati
Previous: Proprietà di media e
Indice
Per quanto riguarda il calcolo della deviazione standard, la sua definizione
potrebbe far supporre che bisognerebbe
trovare prima la media, poi calcolare
gli 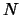 scarti
scarti 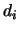 , farne il quadrato, e così via. Questa operazione
è chiaramente lunga e macchinosa e, anche se effettuata con un
calcolatore, richiederebbe di archiviare in memoria tutti i valori di
, farne il quadrato, e così via. Questa operazione
è chiaramente lunga e macchinosa e, anche se effettuata con un
calcolatore, richiederebbe di archiviare in memoria tutti i valori di
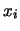 per poterli utilizzare nel calcolo degli scarti.
In realtà è possibile utilizzare una procedura più snella
utilizzando la proprietà del punto 5
del paragrafo 5.5,
che ridimostriamo come esercizio:
per poterli utilizzare nel calcolo degli scarti.
In realtà è possibile utilizzare una procedura più snella
utilizzando la proprietà del punto 5
del paragrafo 5.5,
che ridimostriamo come esercizio:
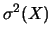 |
 |
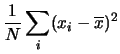 |
(5.29) |
| |
 |
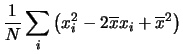 |
(5.30) |
| |
 |
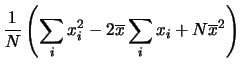 |
(5.31) |
| |
 |
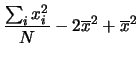 |
(5.32) |
| |
 |
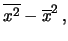 |
(5.33) |
dove
è stata indicata con
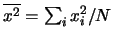 la
media dei quadrati.
Quindi si è trovato che
``la varianza è pari alla media dei quadrati meno il quadrato della
media''. Ricordandosi che il peso statistico dell'
la
media dei quadrati.
Quindi si è trovato che
``la varianza è pari alla media dei quadrati meno il quadrato della
media''. Ricordandosi che il peso statistico dell'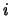 -mo
evento è pari a
-mo
evento è pari a 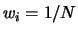 si vede come
la quantità
si vede come
la quantità
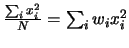 è pari al momento
di inerzia della distribuzione rispetto all'origine delle ascisse,
come era già stato discusso nel paragrafo 5.5
è pari al momento
di inerzia della distribuzione rispetto all'origine delle ascisse,
come era già stato discusso nel paragrafo 5.5
È quindi preferibile calcolare, contemporaneamente a
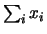 anche
anche
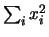 e dalle (5.33) ottenere media
e varianza. Questa è la tecnica utilizzata anche nei programmi al calcolatore
e nelle calcolatrici tascabili con funzioni statistiche. In queste ultime
appositi tasti, generalmente contrassegnati da
e dalle (5.33) ottenere media
e varianza. Questa è la tecnica utilizzata anche nei programmi al calcolatore
e nelle calcolatrici tascabili con funzioni statistiche. In queste ultime
appositi tasti, generalmente contrassegnati da 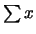 e
e 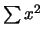 , permettono di leggere il valore raggiunto dopo che
è stato inserito l'
, permettono di leggere il valore raggiunto dopo che
è stato inserito l'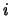 -mo dato. Queste funzioni possono tornare utili
per calcolare valori parziali e totali di media e deviazione standard
di una lunga serie di misure senza dover inserire di nuovo tutti i numeri.
Infatti le sommatorie parziali possono essere annotate e sommate fra di loro
per combinare vari gruppi di dati.
Questo è particolarmente importante quando si ha una lunga serie
di valori: è preferibile annotare di tanto in tanto i risultati parziali
in modo da non dover ricominciare da capo se si commette un errore.
-mo dato. Queste funzioni possono tornare utili
per calcolare valori parziali e totali di media e deviazione standard
di una lunga serie di misure senza dover inserire di nuovo tutti i numeri.
Infatti le sommatorie parziali possono essere annotate e sommate fra di loro
per combinare vari gruppi di dati.
Questo è particolarmente importante quando si ha una lunga serie
di valori: è preferibile annotare di tanto in tanto i risultati parziali
in modo da non dover ricominciare da capo se si commette un errore.
Tabella:
Calcolo dettagliato di medie e varianze dai dati di
conteggio per 3 secondi (tabella 4.1).
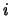 |
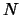 |
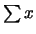 |
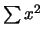 |
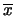 |
 |
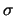 |
| 1-50 |
50 |
24 |
42 |
0.48 |
0.84 |
0.85 |
| 51-100 |
50 |
36 |
60 |
0.72 |
1.20 |
0.83 |
| 1-100 |
100 |
60 |
102 |
0.60 |
1.02 |
0.81 |
|
Come esempio consideriamo i dati del contatore per 3 secondi
e valutiamo media e deviazione standard della distribuzione e delle
due distribuzioni formate dividendo i dati in due campioni.
I risultati sono in tabella 5.2.
Per l'intero campione svolgiamo in dettaglio i conti




Next: Effetto del raggruppamento in
Up: Descrizione quantitativa dei dati
Previous: Proprietà di media e
Indice
Giulio D'Agostini
2001-04-02
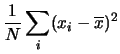
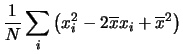
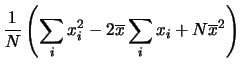
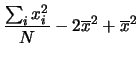
![]() anche
anche
![]() e dalle (5.33) ottenere media
e varianza. Questa è la tecnica utilizzata anche nei programmi al calcolatore
e nelle calcolatrici tascabili con funzioni statistiche. In queste ultime
appositi tasti, generalmente contrassegnati da
e dalle (5.33) ottenere media
e varianza. Questa è la tecnica utilizzata anche nei programmi al calcolatore
e nelle calcolatrici tascabili con funzioni statistiche. In queste ultime
appositi tasti, generalmente contrassegnati da ![]() e
e ![]() , permettono di leggere il valore raggiunto dopo che
è stato inserito l'
, permettono di leggere il valore raggiunto dopo che
è stato inserito l'![]() -mo dato. Queste funzioni possono tornare utili
per calcolare valori parziali e totali di media e deviazione standard
di una lunga serie di misure senza dover inserire di nuovo tutti i numeri.
Infatti le sommatorie parziali possono essere annotate e sommate fra di loro
per combinare vari gruppi di dati.
Questo è particolarmente importante quando si ha una lunga serie
di valori: è preferibile annotare di tanto in tanto i risultati parziali
in modo da non dover ricominciare da capo se si commette un errore.
-mo dato. Queste funzioni possono tornare utili
per calcolare valori parziali e totali di media e deviazione standard
di una lunga serie di misure senza dover inserire di nuovo tutti i numeri.
Infatti le sommatorie parziali possono essere annotate e sommate fra di loro
per combinare vari gruppi di dati.
Questo è particolarmente importante quando si ha una lunga serie
di valori: è preferibile annotare di tanto in tanto i risultati parziali
in modo da non dover ricominciare da capo se si commette un errore.