- Lo spazio degli eventi (indicato da qui in poi con
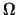 ) è
) è
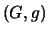 , con tutti gli elementi
equiprobabili.
Si ha quindi con certezza
il genotipo
, con tutti gli elementi
equiprobabili.
Si ha quindi con certezza
il genotipo 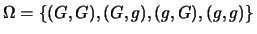 , da cui il carattere giallo.
, da cui il carattere giallo.
- Combinando
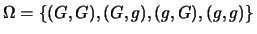 con
con 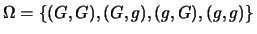 si ottiene
si ottiene
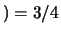 ,
,
da cui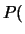 ``giallo''
``giallo''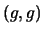 .
.
- Combinando
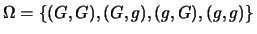 con
con 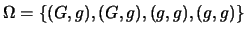 si ottiene
si ottiene
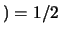 .,
.,
da cui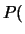 ``giallo''
``giallo''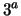 .
.
-
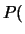 ``verde''
``verde''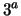 .
.
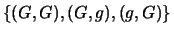 generazione:
combiniamo
generazione:
combiniamo
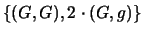 con
sé stesso. Per comodità
riscriviamo lo spazio delle possibilità
con
sé stesso. Per comodità
riscriviamo lo spazio delle possibilità
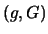 ,
in quanto
,
in quanto 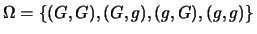 e
e 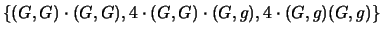 sono indistiguibili.
Il nuovo spazio degli incroci è costituito da:
sono indistiguibili.
Il nuovo spazio degli incroci è costituito da:
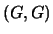 . Si hanno quindi in totale 36 coppie di geni
di cui 16 del tipo
. Si hanno quindi in totale 36 coppie di geni
di cui 16 del tipo 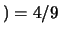 ,
16 del tipo
,
16 del tipo 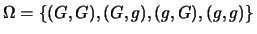 e soltanto 4 del tipo
e soltanto 4 del tipo 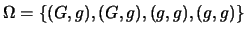 :
:
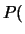 ``Giallo omozigota''
``Giallo omozigota''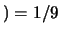 ,
,
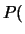 ``Giallo eterozigota''
``Giallo eterozigota''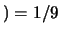 ,
,
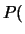 ``Verde''
``Verde''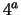 .
.
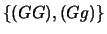 generazione:
I gialli della
generazione:
I gialli della 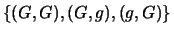 generazione selezionati erano
con pari probabilità omo- e etero-zigoti, quindi combinando
generazione selezionati erano
con pari probabilità omo- e etero-zigoti, quindi combinando
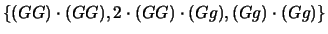 con sé stessi otteniamo
con sé stessi otteniamo
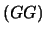 . Delle 16 possibilità,
9 danno luogo a
. Delle 16 possibilità,
9 danno luogo a 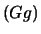 , 6 a
, 6 a 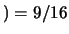 e una sola a
e una sola a 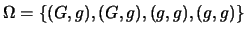 :
:
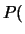 ``Giallo omozigota''
``Giallo omozigota''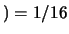 ,
,
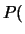 ``Verde''
``Verde''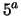 .
.
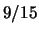 generazione:
Dei gialli della
generazione:
Dei gialli della 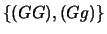 generazione selezionati i
generazione selezionati i 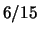 erano
erano
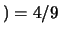 e i
e i 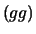 erano
erano 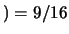 . Si può quindi pensare di combinare
9
. Si può quindi pensare di combinare
9 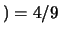 con 6
con 6 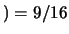 . Delle 900 possibilità ce ne sono 576
. Delle 900 possibilità ce ne sono 576 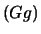 e solo 36
e solo 36 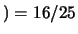 :
:
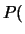 ``Giallo omozigota''
``Giallo omozigota''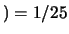 ,
,
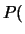 ``Verde''
``Verde''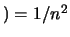 .
.
Da questi esempi si deduce una regola generale valida quando, incrociando due individui provenienti da linee pure, una con allele dominante e l'altra con allele recessivo, si lasciano incrociare nel seguito soltanto gli individui che presentano il carattere dominante:
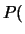 Carattere recessivo
Carattere recessivo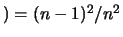 ;
;
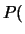 Omozigote dominante
Omozigote dominante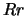 .
.
Per avere piante che diano almeno al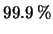 semi gialli
bisogna arrivare a 32 generazioni.
semi gialli
bisogna arrivare a 32 generazioni.
- 0;
- 1/2;
- Si può seguire la percentuale delle caratteristiche al succedersi delle
generazioni con la tabella 16.1, dove sono indicate le frequenza
dei geni e le probabilità, ottenute normalizzando al numero
totale di coppie di geni in ciascuna generazione:
Tabella 16.1: Evoluzione dello spazio delle possibilità dei geni 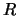 e
e  (vedi testo).
(vedi testo).gen. Rosso Roano Bianco 0 
(1) 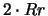
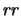
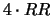
1 RR 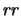
rr (1/4) (1/2) (1/4) 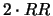
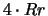
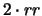
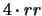
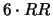
2 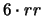
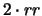
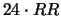
(3/8) (1/4) (3/8) 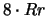
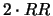
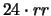
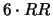
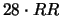
3 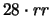
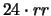
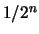
(7/16) (1/8) (7/16) 


La frazione di roani va come
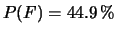 in funzione del numero di
generazione. Questo sistema di incroci, nel caso di non dominanza,
tende a selezionare individui omozigoti.
in funzione del numero di
generazione. Questo sistema di incroci, nel caso di non dominanza,
tende a selezionare individui omozigoti.
In questi casi conviene fare una tabellina del tipo
| fum |
|
fum |
|
| 120 | 480 | 600 | |
| 320 | 80 | 400 | |
| 440 | 560 | 1000 |
In realtà, l'avversario ha il
Dalle quote di scommessa si calcolano
Rispettivamente 4/3 e 4 volte la puntata.
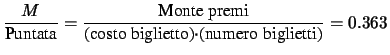 .
.
Speranza matematica:
 .
.
I P
P![$\displaystyle (G(\epsilon)) =
-p\left[1-(p+\epsilon)\right]^2 - (1-p)\left[p+e\right]^2
=$](img3955.png) I
I P
P
Conviene non bluffare (
I P
P![$\displaystyle (G(\epsilon))
= -p\left[1-(p+\epsilon)\right] - (1-p)\left[p+e\right]
=$](img3958.png) I
I P
P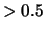
Se