



Next: Bayesian networks
Up: Appendix on probability and
Previous: Biased Bayesian estimators and
Contents
Another prejudice toward Bayesian inference
shared by practitioners who have grown up with
conventional statistics is related to the so-called
`frequentistic coverage'. Since, in my opinion,
this is a kind of condensate of frequentistic
nonsense,8.13
I avoid summarizing it in my own words,
as the risk of distorting something in which
I cannot see any meaning is too high.
A quotation8.14taken from Ref. [68] should clarify the issue:
``Although particle physicists may use the words `confidence
interval' loosely, the most common meaning is still in terms
of original classical concept of ``coverage'' which follows
from the method of construction suggested in Fig. ...
This concept is usually stated (too narrowly, as noted below)
in terms of a hypothetical ensemble of similar experiments,
each of which measures 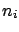 and computes a confidence
interval for
and computes a confidence
interval for 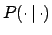 with say, 68% C.L. Then the classical construction
guarantees that in the limit of a large ensemble,
68% of the confidence intervals contain the unknown
true value
with say, 68% C.L. Then the classical construction
guarantees that in the limit of a large ensemble,
68% of the confidence intervals contain the unknown
true value 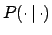 , i.e., they `cover'
, i.e., they `cover' 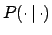 .
This property, called coverage in the frequentistic
sense, is the defining property of classical confidence
intervals. It is important to see this property as what it
is: it reflects the relative frequency with which the statement,
`
.
This property, called coverage in the frequentistic
sense, is the defining property of classical confidence
intervals. It is important to see this property as what it
is: it reflects the relative frequency with which the statement,
`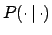 is in the interval
is in the interval
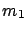 ', is a true
statement. The probabilistic variables
in this statements are
', is a true
statement. The probabilistic variables
in this statements are 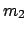 and
and 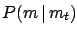 ;
; 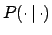 is fixed and unknown.
It is equally important to see what frequentistic coverage is not:
it is a not statement about the degree of belief
that
is fixed and unknown.
It is equally important to see what frequentistic coverage is not:
it is a not statement about the degree of belief
that 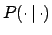 lies within the confidence interval of a particular
experiment. The whole concept of `degree of belief'
does not exist with respect to classical confidence intervals,
which are cleverly (some would say devilishly) defined by a construction
which keeps strictly to statements about
lies within the confidence interval of a particular
experiment. The whole concept of `degree of belief'
does not exist with respect to classical confidence intervals,
which are cleverly (some would say devilishly) defined by a construction
which keeps strictly to statements about
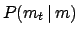 and never uses a probability density in the variable
and never uses a probability density in the variable
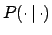 .
.
This strict classical approach can be considered to be either
a virtue or a flaw, but I think that both critics and adherents
commonly make a mistake in describing coverage
from the narrow point of view which I described in the preceeding
paragraph. As Neyman himself pointed out from the beginning,
the concept of coverage is not restricted to the idea
of an ensemble of hypothetical nearly-identical experiments.
Classical confidence intervals
have a much more powerful property: if, in an ensemble of
real, different, experiments, each
experiment measures whatever observables it likes, and
construct a 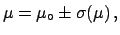 C.L. confidence
interval, then in the long run
C.L. confidence
interval, then in the long run 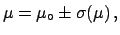 of the confidence intervals cover
the true value of their respective observables. This is directly applicable
to real life, and is the real beauty of classical confidence intervals.''
of the confidence intervals cover
the true value of their respective observables. This is directly applicable
to real life, and is the real beauty of classical confidence intervals.''
I think that the reader can judge for himself whether this approach
seems reasonable. From the Bayesian point of view, the
full answer is provided by
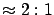 , to use the same notation
of Ref. [68]. If this evaluation has been carried out
under the requirement of coherence, from
, to use the same notation
of Ref. [68]. If this evaluation has been carried out
under the requirement of coherence, from
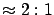 one can
evaluate a probability for
one can
evaluate a probability for 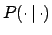 to lie in the
interval
to lie in the
interval 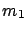 . If this probability is
. If this probability is 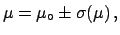 , in order to stick to
the same value this implies:
, in order to stick to
the same value this implies:
- one believes
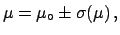 that
that 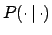 is in that interval;
is in that interval;
- one is ready to place a
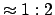 bet on
bet on 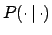 being
in that interval and a
being
in that interval and a
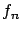 bet on
bet on 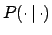 being elsewhere;
being elsewhere;
- if one imagines
 situations in which one
has similar conditions (they could be
different experiments, or simply urns
containing a 68% proportion of white balls)
and thinks of the relative frequency with which one expects
that this statement will be true (
situations in which one
has similar conditions (they could be
different experiments, or simply urns
containing a 68% proportion of white balls)
and thinks of the relative frequency with which one expects
that this statement will be true (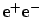 ),
logic applied to the basic rules of probability
imply that, with the increasing
),
logic applied to the basic rules of probability
imply that, with the increasing  ,
it will become more and more improbable that
,
it will become more and more improbable that 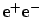 will differ much from
will differ much from 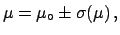 (Bernoulli theorem).
(Bernoulli theorem).
So, the intuitive concept of `coverage' is naturally
included in the Bayesian result and it is expressed in intuitive
terms (probability of true value and expected frequency).
But this result has to depend also on priors,
as seen in the previous section and in many other places in this
report (see, for example, Section ![[*]](file:/usr/lib/latex2html/icons/crossref.png) ). Talking about
coverage independently of prior knowledge (as frequentists do)
makes no sense, and leads to contradictions
and paradoxes. Imagine, for example, an experiment
operated for one hour at LEP200 and reporting
zero candidate events for zirconium production
in
). Talking about
coverage independently of prior knowledge (as frequentists do)
makes no sense, and leads to contradictions
and paradoxes. Imagine, for example, an experiment
operated for one hour at LEP200 and reporting
zero candidate events for zirconium production
in
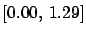 in the absence of expected background.
I do not think that there is a single particle physicist
ready to believe that, if the experiment is repeated
many times, in only 68% of the cases
the 68% C.L. interval
in the absence of expected background.
I do not think that there is a single particle physicist
ready to believe that, if the experiment is repeated
many times, in only 68% of the cases
the 68% C.L. interval
![$ [0.00,\, 1.29]$](img1229.png) will contain
the true value of the `Poisson signal mean', as a
blind use of Table II of Ref. [60] would
imply.8.15
If this example seems a bit odd, I invite you to think
about the many 95% C.L. lower limits on the mass of postulated
particles. Do you really believe that in 95%
of the cases the mass is above the limit, and in 5% of the cases
below the limit? If this is the case, you would bet
$5 on a mass value below the limit, and receive $100 if this
happened to be true (you should be ready to accept the bet,
since, if you believe in frequentistic coverage, you must admit that
the bet is fair). But perhaps you will never accept such a bet
because you believe much more than 95% that the
mass is above the limit, and then the bet is not fair at all;
or because you are aware of thousands of lower limits, and
a particle has never shown up on the 5% side...
will contain
the true value of the `Poisson signal mean', as a
blind use of Table II of Ref. [60] would
imply.8.15
If this example seems a bit odd, I invite you to think
about the many 95% C.L. lower limits on the mass of postulated
particles. Do you really believe that in 95%
of the cases the mass is above the limit, and in 5% of the cases
below the limit? If this is the case, you would bet
$5 on a mass value below the limit, and receive $100 if this
happened to be true (you should be ready to accept the bet,
since, if you believe in frequentistic coverage, you must admit that
the bet is fair). But perhaps you will never accept such a bet
because you believe much more than 95% that the
mass is above the limit, and then the bet is not fair at all;
or because you are aware of thousands of lower limits, and
a particle has never shown up on the 5% side...




Next: Bayesian networks
Up: Appendix on probability and
Previous: Biased Bayesian estimators and
Contents
Giulio D'Agostini
2003-05-15
and computes a confidence interval for
with say, 68% C.L. Then the classical construction guarantees that in the limit of a large ensemble, 68% of the confidence intervals contain the unknown true value
, i.e., they `cover'
. This property, called coverage in the frequentistic sense, is the defining property of classical confidence intervals. It is important to see this property as what it is: it reflects the relative frequency with which the statement, `
is in the interval
', is a true statement. The probabilistic variables in this statements are
and
;
is fixed and unknown. It is equally important to see what frequentistic coverage is not: it is a not statement about the degree of belief that
lies within the confidence interval of a particular experiment. The whole concept of `degree of belief' does not exist with respect to classical confidence intervals, which are cleverly (some would say devilishly) defined by a construction which keeps strictly to statements about
and never uses a probability density in the variable
.
C.L. confidence interval, then in the long run
of the confidence intervals cover the true value of their respective observables. This is directly applicable to real life, and is the real beauty of classical confidence intervals.''
![$ [0.00,\, 1.29]$](img1229.png) will contain
the true value of the `Poisson signal mean', as a
blind use of Table II of Ref. [60] would
imply.8.15
If this example seems a bit odd, I invite you to think
about the many 95% C.L. lower limits on the mass of postulated
particles. Do you really believe that in 95%
of the cases the mass is above the limit, and in 5% of the cases
below the limit? If this is the case, you would bet
$5 on a mass value below the limit, and receive $100 if this
happened to be true (you should be ready to accept the bet,
since, if you believe in frequentistic coverage, you must admit that
the bet is fair). But perhaps you will never accept such a bet
because you believe much more than 95% that the
mass is above the limit, and then the bet is not fair at all;
or because you are aware of thousands of lower limits, and
a particle has never shown up on the 5% side...
will contain
the true value of the `Poisson signal mean', as a
blind use of Table II of Ref. [60] would
imply.8.15
If this example seems a bit odd, I invite you to think
about the many 95% C.L. lower limits on the mass of postulated
particles. Do you really believe that in 95%
of the cases the mass is above the limit, and in 5% of the cases
below the limit? If this is the case, you would bet
$5 on a mass value below the limit, and receive $100 if this
happened to be true (you should be ready to accept the bet,
since, if you believe in frequentistic coverage, you must admit that
the bet is fair). But perhaps you will never accept such a bet
because you believe much more than 95% that the
mass is above the limit, and then the bet is not fair at all;
or because you are aware of thousands of lower limits, and
a particle has never shown up on the 5% side...