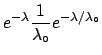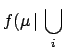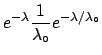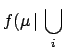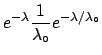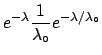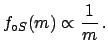Next: Constraining the mass of
Up: Unbiased results
Previous: Unbiased results
Contents
Uniform prior and fictitious quantities
Let us consider  independent data sets, or experiments, each of which gives
information on the quantity
independent data sets, or experiments, each of which gives
information on the quantity  . For each data set there is a
likelihood
. For each data set there is a
likelihood
data
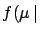
Each data set gives, by itself, the following information:
The global inference is obtained
using Bayes' theorem iteratively:
We may use, as a formal tool, a ficticious
inference
 using for each data set a uniform prior in the range
using for each data set a uniform prior in the range
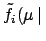 :
:
This allows us to rewrite
This stratagem has the advantage that one can
report `pseudoresults' on fictitious quantities which,
in the case of Gaussian likelihoods, may be combined
according to the usual formula of the average with the
inverse of the variances (see Section ![[*]](file:/usr/lib/latex2html/icons/crossref.png) ).
They can be transformed, finally, into the physical result
using the physical prior
).
They can be transformed, finally, into the physical result
using the physical prior
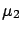 . It is important
to state the procedure clearly and, if possible, to indicate
the fictitious quantity with different symbols.
For example, the result of the problem of Section
. It is important
to state the procedure clearly and, if possible, to indicate
the fictitious quantity with different symbols.
For example, the result of the problem of Section ![[*]](file:/usr/lib/latex2html/icons/crossref.png) can be reported in the following way:
can be reported in the following way:
``From the observed value of -5.4eV and the knowledge
of the likelihood,
described by a normal distribution centred in the
true value of the mass
with
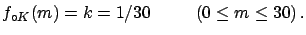
eV independent of the mass, we get
a fictitious mass of
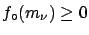
eV
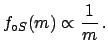
where `fictitious' indicates a hypothetical mass
which could assume any real number with uniform distribution.
Assuming the more physical hypothesis
 yields to ...(see figure ...), from which follows a 95%
upper limit of 3.9eV.''
The conclusion of this section is that the uniform prior
is a convenient prior for many purposes:
yields to ...(see figure ...), from which follows a 95%
upper limit of 3.9eV.''
The conclusion of this section is that the uniform prior
is a convenient prior for many purposes:
- it produces results very similar to those
obtainable using the rational priors of those who have
done the experiment, as shown in many of the examples
given in these notes (see, for example, Section
![[*]](file:/usr/lib/latex2html/icons/crossref.png) );
);
- it allows easy combination of data and a physics motivated prior
can be added at the end;
- there is no problem of `double counting' the same prior,
as would happen if several experimenters were to use the same
non-uniform prior to infer the same quantity from different data.
The problem of presenting unbiased results in frontier measurements
is also discussed in Refs. [26], [25],
[83] and [84].




Next: Constraining the mass of
Up: Unbiased results
Previous: Unbiased results
Contents
Giulio D'Agostini
2003-05-15