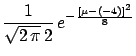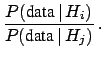
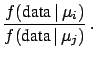 . In this case one may also calculate Bayes' factors
between any pair of values
. In this case one may also calculate Bayes' factors
between any pair of values
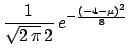
When one publishes a likelihood function this should be clearly
stated.
Otherwise the temptation to turn
![]() data
data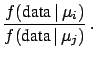 into
into
![]() data
data![]() is really strong. In fact, taking the
example of the neutrino mass of Section
is really strong. In fact, taking the
example of the neutrino mass of Section ![]() ,
the formula
,
the formula