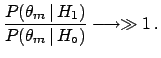Next: Frequentists and Bayesian `sects'
Up: Appendix on probability and
Previous: Bayesian networks
Contents
Why do frequentistic hypothesis tests `often work'?
The problem of classifying hypotheses according to their
credibility is natural in the Bayesian framework.
Let us recall briefly the following way of
drawing conclusions
about two hypotheses in the light of some data:
This form is very convenient, because:
- it is valid even if the hypotheses
 do not form
a complete class [a necessary condition if, instead, one wants to give
the result in the standard form
of Bayes' theorem given by formula (
do not form
a complete class [a necessary condition if, instead, one wants to give
the result in the standard form
of Bayes' theorem given by formula (![[*]](file:/usr/lib/latex2html/icons/crossref.png) )];
)];
- it shows that the Bayes factor is an unbiased way of reporting
the result (especially if a different initial probability
could substantially change
the conclusions);
- the Bayes factor depends only on the likelihoods of observed data
and not at all on unobserved data (contrary to what happens in conventional
statistics, where conclusions depend on the probability
of all the configurations of data in the tails of the
distribution8.16). In other words, Bayes' theorem
applies in the form (
![[*]](file:/usr/lib/latex2html/icons/crossref.png) ) and not as
) and not as
- testing a single hypothesis does not make sense: one may talk
of the probability of the Standard Model (SM) only if one is considering
an Alternative Model (AM), thus getting,
for example,
 can be arbitrarily small, but
if there is not
a reasonable alternative one has only to accept the fact
that some events have been observed which are very far
from the expectation value;
can be arbitrarily small, but
if there is not
a reasonable alternative one has only to accept the fact
that some events have been observed which are very far
from the expectation value;
- repeating what has been said several times, in the
Bayesian scheme the conclusions depend only on observed
data and on previous knowledge;
in particular, they do not depend on
- how the
data have been combined;
- data not observed and considered to be even rarer than the observed
data;
- what the experimenter was planning to do before
starting to take data. (I am referring to predefined fiducial cuts and the
stopping rule, which, according to the frequentistic
scheme should be defined in the test protocol.
Unfortunately I cannot discuss this matter here in
detail and I recommend the reading of Ref. [10]).
At this point we can finally reply to the
question: ``why do commonly-used
methods of hypothesis testing usually work?''
(see Sections ![[*]](file:/usr/lib/latex2html/icons/crossref.png) and
and ![[*]](file:/usr/lib/latex2html/icons/crossref.png) ).
).
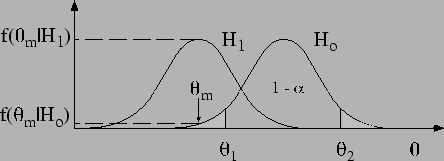
Figure:
Testing a hypothesis  implies that
one is ready to replace it with an alternative hypothesis.
implies that
one is ready to replace it with an alternative hypothesis.
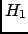 |
By reference to Fig. ![[*]](file:/usr/lib/latex2html/icons/crossref.png) (imagine for a
moment the figure without the curve
(imagine for a
moment the figure without the curve 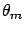 ), the argument that
), the argument that
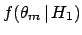 provides evidence against
provides evidence against  is intuitively
accepted and often works, not (only) because of
probabilistic considerations of
is intuitively
accepted and often works, not (only) because of
probabilistic considerations of 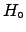 in the light of
in the light of 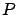 , but because it is often reasonable
to imagine an alternative hypothesis
, but because it is often reasonable
to imagine an alternative hypothesis 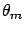 that
that
- maximizes the likelihood
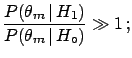 or, at least
or, at least
- has a comparable prior [
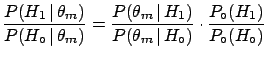 ],
such that
],
such that
So, even though
there is no objective or logical reason why
the frequentistic scheme should work, the reason why it often does
is that in many cases the test is made when one has
serious doubts about the null hypothesis.
But a peak appearing
in the middle of a distribution, or any excess of events, is not,
in itself, a hint of new physics (Fig. ![[*]](file:/usr/lib/latex2html/icons/crossref.png) is an invitation to meditation...).
is an invitation to meditation...).
Figure:
Experimental obituary (courtesy of Alvaro de
Rujula[71]).
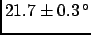 |
My recommendations are therefore the following.
- Be very careful when drawing conclusions from
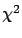 tests, `3
tests, `3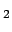 golden rule', and other `bits of magic';
golden rule', and other `bits of magic';
- Do not pay too much attention to fixed rules suggested by statistics
`experts', supervisors, and
even Nobel laureates, taking also into account that
- they usually have permanent positions and risk less
than PhD students
and postdocs who do most of the real work;
- they have been `miseducated' by the exciting experience
of the glorious 1950s to 1970s: as Giorgio Salvini says,
``when I was young, and it was possible to go to sleep at
night after having added within the day some important
brick to the building of the elementary particle palace.
We were certainly lucky.''[72]. Especially when they were hunting
for resonances, priors were very high, and the 3-4
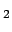 rule
was a good guide.
rule
was a good guide.
- Fluctuations exist. There are millions of frequentistic tests
made every year in the world. And there is no probability
theorem ensuring that the most extreme fluctuations
occur to a precise Chinese student,
rather than to a large HEP collaboration (this is the same
reasoning of many Italians who buy national lotteria
tickets in Rome or in motorway restaurants,
because `these tickets win more often'...).
As a conclusion to these remarks, and to invite the reader to take with much care the assumption
of equiprobability of hypothesis (a hidden assumption in many frequentistic methods), I would like
to add this quotation by Poincaré [6]:
``To make my meaning clearer, I go back to the game of écarté mentioned
before.8.17 My adversary deals for the first time and
turns up a king. What is the probability that he is a sharper? The formulae ordinarily taught give 8/9,
a result which is obviously rather surprising. If we look at it closer, we see that the
conclusion is arrived at as if, before sitting down at the table, I had considered that there was
one chance in two that my adversary was not honest. An absurd hypothesis, because in that case I
should certainly not have played with him; and this explains the absurdity of the conclusion. The
function on the à priori probability was unjustified, and that is why the conclusion of the
à posteriori probability led me into an inadmissible result. The importance of this
preliminary convention is obvious. I shall even add that if none were made, the problem of the
à posteriori probability would have no meaning. It must be always made either explicitly or tacitly.''




Next: Frequentists and Bayesian `sects'
Up: Appendix on probability and
Previous: Bayesian networks
Contents
Giulio D'Agostini
2003-05-15
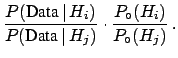
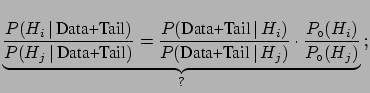
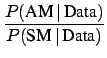
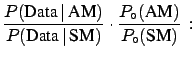
 can be arbitrarily small, but
if there is not
a reasonable alternative one has only to accept the fact
that some events have been observed which are very far
from the expectation value;
can be arbitrarily small, but
if there is not
a reasonable alternative one has only to accept the fact
that some events have been observed which are very far
from the expectation value;
![]() (imagine for a
moment the figure without the curve
(imagine for a
moment the figure without the curve ![]() ), the argument that
), the argument that
![]() provides evidence against
provides evidence against ![]() is intuitively
accepted and often works, not (only) because of
probabilistic considerations of
is intuitively
accepted and often works, not (only) because of
probabilistic considerations of ![]() in the light of
in the light of ![]() , but because it is often reasonable
to imagine an alternative hypothesis
, but because it is often reasonable
to imagine an alternative hypothesis ![]() that
that
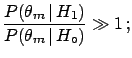 or, at least
or, at least
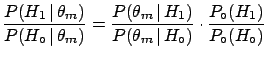 ],
such that
],
such that