



Next: Unbiased results
Up: Poisson model: dependence on
Previous: Is there a signal?
Contents
Signal and background: a Mathematica example
As a last application of the Poissonian model, let us make a
numerical example of a counting measurement in the presence of background.
To compare full and approximative results, let us choose a
number large enough for the normal approximation
to be reasonable. For example, we have observed 44 counts with an expected
background of 28 counts. What can we tell about the signal?
We solve the problem with the following Mathematica
code9.3
applied to the formulae of Section ![[*]](file:/usr/lib/latex2html/icons/crossref.png) (
(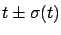 stands for
stands for 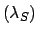 and
and 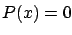 for
for
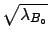 ):
):
(********************************************************)
ClearAll["Global`*"]
f = (Exp[-s]*(b0+s)^x)/(x!Sum[b0^i/i!, {i, 0, x}])
x=44;
b0=28;
m = NIntegrate[s*f, {s, 0, 1E^6}]
sigma = Sqrt[NIntegrate[s^2*f, {s, 0, 1E^6}] - m^2]
Plot[f, {s, 0, 50}, AxesLabel->{s, "f"}]
fd1=D[Log[f], s];
fd2= D[fd1, s];
res=FindMinimum[-f, {s,m}];
smax = res[[2]]
sigma2=1/Sqrt[-(fd2 /. res[[2]])]
(********************************************************)
The code evaluates and plots
the final distribution of 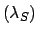 obtained from a uniform prior [formula (
obtained from a uniform prior [formula (![[*]](file:/usr/lib/latex2html/icons/crossref.png) )]
and calculates:
)]
and calculates:
- the prevision
E
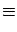
m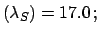
E
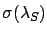
- the standard deviation
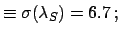 :
:
sigma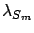
- the mode
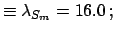 :
:
smax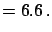
- the approximated standard deviation calculated from
the shape of the final distribution around the mode
(see Section
![[*]](file:/usr/lib/latex2html/icons/crossref.png) ):
):
sigma2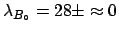
The resulting probability density function for the signal
is shown in Fig. ![[*]](file:/usr/lib/latex2html/icons/crossref.png) .
.
The approximate, but still Bayesian, reasoning to get the same result
is as follows.
- Given this status of information, the certain quantities are:
- The average value of the background:
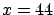 ;
;
- The observation
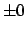 (it does not even make sense to write
(it does not even make sense to write 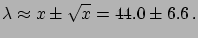 :
44 is 44 !).
:
44 is 44 !).
- Instead, we are uncertain on the parameter
 of the Poissonian
distribution responsible for the observed number of counts;
we can infer [see (
of the Poissonian
distribution responsible for the observed number of counts;
we can infer [see (![[*]](file:/usr/lib/latex2html/icons/crossref.png) ) and (
) and (![[*]](file:/usr/lib/latex2html/icons/crossref.png) )]
)]
- Since
 is due to the contribution of the signal and background,
we have, finally:
is due to the contribution of the signal and background,
we have, finally:
The last evaluation is an example of how Bayesian reasoning
helps, independently of explicit use of Bayes' theorem.
Nevertheless, these results are still conditioned by the assumption
that the signal looked for exists. In fact, Fig.
![[*]](file:/usr/lib/latex2html/icons/crossref.png) does not really prove, from a logical point
of view, that the signal does exist, although the distribution
seems so nicely separated from zero (see also Ref. [25]).
does not really prove, from a logical point
of view, that the signal does exist, although the distribution
seems so nicely separated from zero (see also Ref. [25]).
Figure:
Final distribution for the signal (
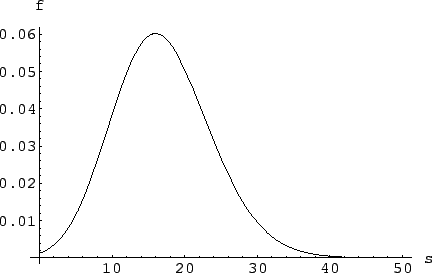 ),
having observed 44 counts, with an expected background of 28
counts.
),
having observed 44 counts, with an expected background of 28
counts.
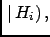 |




Next: Unbiased results
Up: Poisson model: dependence on
Previous: Is there a signal?
Contents
Giulio D'Agostini
2003-05-15
![]() obtained from a uniform prior [formula (
obtained from a uniform prior [formula (![]() )]
and calculates:
)]
and calculates: