



Next: Interpretation of the results
Up: Constraining the mass of
Previous: Naïve procedure
Contents
In order to solve the problem consistently with our beliefs, we
have to avoid the intermediate
inference9.5
on  ,
and write prior and likelihood directly in terms
of
,
and write prior and likelihood directly in terms
of 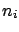 :
:
![$\displaystyle f(m\,\vert\,x=0) \propto \exp{\left[-k\,\left(1-\frac{m^2}{E_b^2}\right)^{\frac{3}{2}}\right]} \cdot f_\circ(m)\,,$](img1506.png) |
(9.18) |
with
 constant.
Let us do it again with Mathematica:
constant.
Let us do it again with Mathematica:
(********************************************************)
(* Now let's do it right: *)
lik=Exp[-lambda]
norm=NIntegrate[lik, {m, 0, eba}]
(* fa(m) is the final distribution from experiment A,
under the condition that m < eba *)
fa=lik/norm
Plot[fa, {m, 0.06, eba}, AxesLabel -> {m, f}]
(********************************************************)
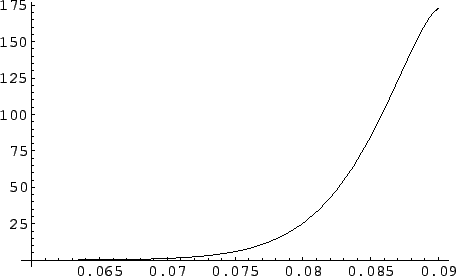
Figure:
Inference on 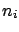 obtained from a direct inference
on
obtained from a direct inference
on 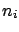 , starting from a uniform prior in this quantity.
, starting from a uniform prior in this quantity.
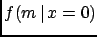 |
The final distribution is shown in Fig. ![[*]](file:/usr/lib/latex2html/icons/crossref.png) .
It is now reasonable and consistent with the expectations:
The values of mass which are less believable are those which could
have been produced easier, given the kinematics. From
.
It is now reasonable and consistent with the expectations:
The values of mass which are less believable are those which could
have been produced easier, given the kinematics. From
 we can calculate several results, for example
a 95% upper limit, the average and the standard deviation:
we can calculate several results, for example
a 95% upper limit, the average and the standard deviation:
(********************************************************)
NIntegrate[fa, {m, 0, 0.0782}]
ava = NIntegrate[m*fa, {m, 0, eba}]
stda = Sqrt[NIntegrate[m*fa, {m, 0, eba}] - ava^2]
(********************************************************)
We get:
 |
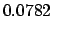 |
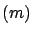 with 95% probability with 95% probability |
(9.19) |
E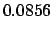 |
 |
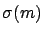 |
(9.20) |
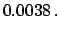 |
 |
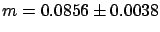 |
(9.21) |




Next: Interpretation of the results
Up: Constraining the mass of
Previous: Naïve procedure
Contents
Giulio D'Agostini
2003-05-15
 constant.
Let us do it again with Mathematica:
constant.
Let us do it again with Mathematica: