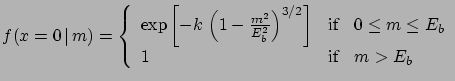``A 95% confidence level lower bound ofmay be misleading, because it transmits information which is inconsistent with the experimental observation. The interpretation of the result (is obtained for the mass of the Standard Model Higgs boson.''[85]
What are our rational beliefs on ![]() , on the basis of experiment A,
releasing the condition
, on the basis of experiment A,
releasing the condition
![]() ?
The data cannot help much because
there is no experimental sensitivity, and the conclusions depend
essentially on the priors.
?
The data cannot help much because
there is no experimental sensitivity, and the conclusions depend
essentially on the priors.
To summarize, the result of the inference is:
As a final remark on the presentation of the result, I would like
to comment on the three significative digits with which the result
on the `conditional lower bound' has been given.
For the sake of the exercise the mass bound has been
evaluated from the condition (![]() ).
But does it really matter if the limit is 0.0782,
rather than 0.0780, or 0.0800?
As stated in Sections
).
But does it really matter if the limit is 0.0782,
rather than 0.0780, or 0.0800?
As stated in Sections ![]() and
and ![]() ,
the limits have to be considered in the same way as the uncertainty.
Nobody cares if the uncertainty of the uncertainty is 10 or 20%,
and nobody would redo a MACRO-like experiment to lower the monopole
limit by 20%. Simply translating this argument
to the case under study, it may give the impression that one significant
digit would be enough (0.08), but this is not true, if
we stick to presenting the result under the condition that
,
the limits have to be considered in the same way as the uncertainty.
Nobody cares if the uncertainty of the uncertainty is 10 or 20%,
and nobody would redo a MACRO-like experiment to lower the monopole
limit by 20%. Simply translating this argument
to the case under study, it may give the impression that one significant
digit would be enough (0.08), but this is not true, if
we stick to presenting the result under the condition that ![]() is smaller
than
is smaller
than ![]() . In fact, what really matters, is not the absolute
mass, but the mass difference with respect to the kinematical limit.
If the experiment ran with infinite statistics
and found `nothing', there is no interest in providing a detailed
study for the limit:
it will be exactly the same as the kinematical limit. Therefore, the
interesting piece of
information that the experimenter should provide is how far
the lower bound is from the kinematical limit, i.e.
what really matters is not the absolute mass scale,
but rather the mass difference. In our case we have
. In fact, what really matters, is not the absolute
mass, but the mass difference with respect to the kinematical limit.
If the experiment ran with infinite statistics
and found `nothing', there is no interest in providing a detailed
study for the limit:
it will be exactly the same as the kinematical limit. Therefore, the
interesting piece of
information that the experimenter should provide is how far
the lower bound is from the kinematical limit, i.e.
what really matters is not the absolute mass scale,
but rather the mass difference. In our case we have
| (9.23) |