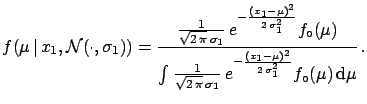Next: Combination of several measurements
Up: Normally distributed observables
Previous: Normally distributed observables
Contents
Final distribution, prevision and credibility intervals of
the true value
The first application of the Bayesian inference will be that
of a normally distributed quantity. Let us take
a data sample
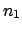 of
of 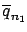 measurements, of which
we calculate the average
measurements, of which
we calculate the average
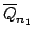 . In our formalism
. In our formalism
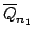 is a realization of the random variable
is a realization of the random variable
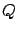 . Let us assume we know the
standard deviation
. Let us assume we know the
standard deviation 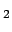 of the variable
of the variable 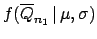 , either
because
, either
because 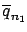 is very large and can be estimated
accurately from the sample or because it was known a priori
(We are not going to discuss in these notes the case
of small samples and unknown variance5.2.)
is very large and can be estimated
accurately from the sample or because it was known a priori
(We are not going to discuss in these notes the case
of small samples and unknown variance5.2.) The property of the average (see Section
The property of the average (see Section ![[*]](file:/usr/lib/latex2html/icons/crossref.png) )
tells us that the
likelihood
)
tells us that the
likelihood
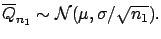 is Gaussian:
is Gaussian:
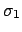 |
(5.11) |
To simplify the following notation, let us call 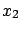 this average and
this average and 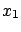 the standard deviation of the average:
the standard deviation of the average:
We then apply (![[*]](file:/usr/lib/latex2html/icons/crossref.png) ) and get
) and get
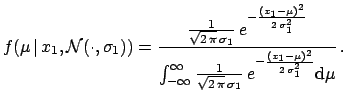 |
(5.14) |
At this point we have to make a choice for
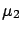 . A reasonable choice
is to take, as a first guess,
a uniform distribution defined over a ``large''
interval which includes
. A reasonable choice
is to take, as a first guess,
a uniform distribution defined over a ``large''
interval which includes 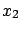 . It is not really important
how large the interval is,
for a few
. It is not really important
how large the interval is,
for a few 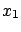 away
from
away
from 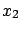 the integrand at the denominator
tends to zero because of the Gaussian function. What is important
is that a constant
the integrand at the denominator
tends to zero because of the Gaussian function. What is important
is that a constant
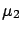 can be simplified
in (
can be simplified
in (![[*]](file:/usr/lib/latex2html/icons/crossref.png) ), obtaining
), obtaining
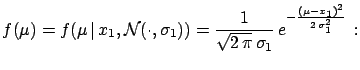 |
(5.15) |
The integral in the denominator is equal to unity, since
integrating with
respect to  is equivalent to integrating with respect to
is equivalent to integrating with respect to 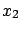 .
The final result is then
.
The final result is then
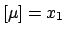 |
(5.16) |
- the true value is normally distributed around
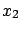 ;
;
- its best estimate (prevision) is
E
![$ [\mu]=x_1$](img662.png) ;
;
- its variance is
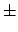 ;
;
- the ``confidence intervals'', or credibility intervals,
in which there is a certain probability of finding the
true value are easily calculable:
| Probability level |
credibility interval |
| (confidence level) |
(confidence interval) |
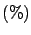 |
|
| 68.3 |
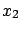 |
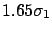 |
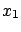 |
| 90.0 |
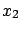 |
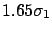 |
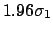 |
| 95.0 |
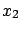 |
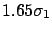 |
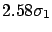 |
| 99.0 |
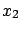 |
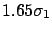 |
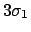 |
| 99.73 |
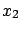 |
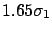 |
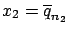 |




Next: Combination of several measurements
Up: Normally distributed observables
Previous: Normally distributed observables
Contents
Giulio D'Agostini
2003-05-15