Si tratta del caso d) di figura 9. Di questo si è già tenuto conto, implicitamente, quando è stata valutata
- L'errore di zero, sia esso sulle ascisse che sulle ordinate,
non ha nessuna influenza sul coefficiente angolare,
in quanto esso è valutato come rapporto di diferenze:
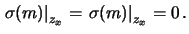
- Un errore di zero sulle ordinate (
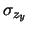 )
si riflette direttamente
sul valore dell'intercetta, in quanto tutti
i punti potrebbero essere traslati coerentemente verso l'alto o verso
il basso. Quindi il contributo a
)
si riflette direttamente
sul valore dell'intercetta, in quanto tutti
i punti potrebbero essere traslati coerentemente verso l'alto o verso
il basso. Quindi il contributo a 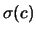 è
è
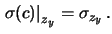
- Un errore di zero sulle ascisse (
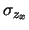 ) causerebbe
una traslazione orizzontale di
tutti i punti. Quindi esso si riflette sull'intercetta
attraverso la pendenza della retta. Ne segue che
il contributo a
) causerebbe
una traslazione orizzontale di
tutti i punti. Quindi esso si riflette sull'intercetta
attraverso la pendenza della retta. Ne segue che
il contributo a 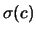 è (trascurando l'effetto di
ordine superiore dovuto all'incertezza sulla pendenza stessa):
è (trascurando l'effetto di
ordine superiore dovuto all'incertezza sulla pendenza stessa):
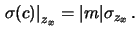
Per capire il comportamento degli errori di scala, sia sulle ascisse che sulle ordinate, consideriamo due punti sulla retta
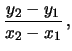 |
(43) | ||
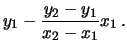 |
(44) |
Consideriamo ora i fattori di scala
e inseriamoli esplicitamente nelle espressioni di
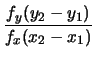 |
|||
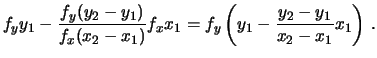 |
Ne concludiamo quindi che
- Il coefficiente angolare risente allo stesso modo
dei due fattori di scala:
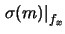

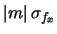
(45) 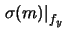

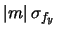
(46)
- L'errore di scala sulle ascisse è ininfluente
sull'intercetta, mentre quello sulle ordinate
vi si riflette proporzionalmente:
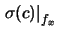

0 (47) 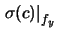

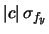
(48)
Eventuali deviazioni dalla linearità degli strumenti si riflettono su una deviazione dalla linearità dell'andamento. Non è possibile dare delle regolette ad hoc. Qualora si notino tali effetti nei punti sperimentali, bisogna cercare di capire se l'effetto è da attribuire a uno dei due strumenti (o a entrambi), oppure è la legge fisica ad essere inadeguata, o si tratta soltanto di una fluttuazione. Si cerca quindi di sostituire o ricalibrare gli strumenti, di apportare correzioni fenomenologicamente giustificate ai dati sperimentali, oppure si utilizza semplicemente la zona nella quale ci sono dei buoni motivi per presupporre che l'andamento sia quello ipotizzato. Un caso macroscopico è quello del grafico dell'allungamento in funzione della massa di figura 10: la molla non si allunga affatto al di sotto di una massa critica (