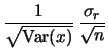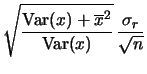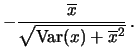Analisi grafica

Vediamo quali sono i passi necessari per un'analisi grafica che, condotta a termine fino in fondo, produce risultati quantitativi in accordo con quelli ottenibili mediante fit con i minimi quadrati. In molte esperienze, comunque, non è necessario procedere ad un'analisi così accurata come quella proposta (vedi discussione nel paragrafo 24) e ci si può fermare al primo passo.

Stima dei parametri

• Si traccia ad occhio la retta, cercando di passare in mezzo a tutti i punti. Questa retta praticamente coincide con quella che si ottiene con i minimi quadrati.
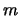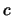• Si ricavano quindi dal grafico due punti che giacciono sulla retta, che siano ben distanziati e ben leggibili. Da questi si ricavano $m$ e $c$ (l'intercetta si ottiene in genere più agelvomente in modo diretto, come è ben noto).

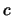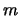  Per quanto riguarda le cifre con cui rileggere i valori si noti come i punti della retta sono ``più stabili'' di quelli delle singole misure e quindi possono essere riletti anche con una cifra in più. Si ottengono quindi $c$ e $m$ con il numero di cifre che seguono dalle solite regolette sulle cifre significative.

Stima dell'incertezza sui parametri ripetendo le misure

Il modo più semplice, e che per le prime esperienze è indubbiamente istruttivo, è quello di ripetere più volte la misura e studiare le fluttuazioni dei risultati. Si tenga conto che, non facendo calcoli di ``errori massimi'' né propagazioni varie, è molto facile ripetere più volte le misure in alcune ore.

Stima dell'incertezza della singola misura dai residui

Figura 11: Residui e barre di incertezza ( $\pm \sigma _r$).

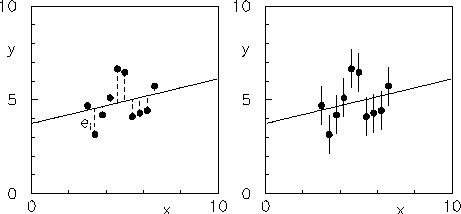
In realtà non c'è alcun bisogno di ripetere le serie di misure. Se ciascuna serie contiene un numero sufficiente di punti (tipicamente, leggermente superiore al numero di parametri che si vogliono valutare) essa racchiude in sé le informazioni necessarie alla valutazione delle incertezze, o almeno a quelle derivanti da errori casuali, mediante il metodo dei residui. Una volta tracciata la retta si può leggere dal grafico, per ogni punto, il residuo $e_i$, ovvero la differenza fra l'ordinata misurata e il valore della retta in corrispondenza dell'ascissa misurata, come mostrato in figura 11. Si ottiene quindi, dalla media dei quadrati dei residui, la stima della deviazione standard delle ordinate, assumendo che sia la stessa per tutti i punti e attribuendo soltanto alle ordinate le deviazioni dal valore vero:

$$\sigma_r = \sqrt{ \frac{\sum_{i=1}^n e_i^2}{n-2}}\,.$$

Il nome $\sigma _r$ sta a indicare sia che essa è calcolato dai residui sia che rappresenta l'equivalente della deviazione standard di ripetitività delle misure. Il fattore $n-2$ al posto di $n$ ha la stessa giustificazione dell'$n-1$ nella deviazione standard, tenendo conto che ora ci sono due vincoli fra i dati. Ripetiamo ancora una volta quanto detto a proposito di $\sigma_{n-1}$: anche se le ragioni profonde di questa scelta non sono sempre condivisibili, il risultato ``va nella direzione giusta''. Anche qui, quando $n$ è dell'ordine della decina, la correzione è ininfluente ai fini pratici.

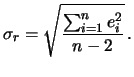
A questo punto, finalmente si conosce l'errore casuale sulle ordinate in condizioni di ripetività (nell'ipotesi che quello sulle ascisse sia trascurabile)!

Ovviamente, si può anche fare l'esercizio opposto e attribuire tutto l'errore alle ascisse (senza dover fare tutti i conti, si può propagare $\sigma _r$ su `` $\sigma_{r_x}$'' mediante la derivata: $\sigma_{r_x}=\sigma_r/\vert m\vert$). E' interessante notare che, anche se il punto di vista cambia drasticamente, saranno invarianti le conclusioni sulle grandezze fisiche di interesse, legate a coefficiente angolare e intercetta.

Valutazione semplificata di $\sigma _r$

Spesso non c'è tempo per rileggere tutti i punti della retta e calcolare $\sigma _r$ dalla somma dei quadrati dei residui. Oppure, semplicemente, ci si accontenta di una sua stima al 20-30%, (sembra tanto, ma anche un'incertezza del 50% su $\sigma _r$ è più che accettabile per molte applicazioni, specialmente se essa è ottenibile in tempi rapidi). In questi casi si possono tracciare, simmetricamente alla retta di migliore stima, due rette parallele tali che contengano i 2/3 circa dei punti. La distanza, lungo l'asse delle ascisse, fra le due rette è approsimativamente uguale a $\sigma _r$. Analogalmente, si possono considerare la ``quasi totalità'' dei punti, e considerarlo un intervallo a 2 o a 3 deviazioni standard.

Barre di incertezza

Soltanto a questo punto è lecito riportare le barre di incertezza sui punti del grafico. Ogni barretta verticale è centrata sul punto sperimentale ed ha lunghezza $2\,\sigma_r$.

Incertezza dei parametri mediante $\sigma _r$ ricavata dai dati

Nota la deviazione standard da attribuire alle singole fluttuazioni delle $y$, si possono usare le formule delle incertezza che si ricavano dal metodo dei minimi quadrati, che qui riportiamo per comodità, riscritte in termini delle grandezze che si conoscono e di quanto altro sia facilmente valutabile per via grafica:

$$\sigma(m) = \frac{1}{\sqrt{\mbox{Var}(x)}} \,\frac{\sigma_r}{\sqrt{n}}$$ (40)

$$\sigma(c) = \sqrt{\frac{\mbox{Var}(x)+\overline{x}^2} {\mbox{Var}(x)}}\, \frac{\sigma_r}{\sqrt{n}}$$ (41)

$$\rho(m,c) = -\frac{\overline{x}}{\sqrt{\mbox{Var}(x)+\overline{x}^2}}\,.$$ (42)

Si noti che Var$(x)$ non è legata alle incertezze sulle $X$ (convenzionalmente nulle): essa misura invece la dispersione delle $x$ e la sua radice quadrata è legata al cosiddetto ``braccio di leva'' dei dati sperimentali. E' interessante notare come questo possa essere valutato agevolmente dal grafico se i punti sono circa spaziati lungo l'ascissa (caso tipico delle esercitazioni di laboratorio). Approssimando i punti sperimentali ad una distribuzione uniforme si ottiene infatti³⁸

$$\sqrt{\mbox{Var}(x)} \approx \frac{x_{max}-x_{min}}{\sqrt{12}}\,.$$

Si faccia inoltre attenzione a non confondere il coefficiente di correlazione fra i parametri (indicato con $\rho(m,c)$) con il coefficiente di correlazione fra ascisse e ordinate dei punti sperimentali (indicato con $\rho(x,y)$): la grandezza di interesse ai fini del risultato è $\rho(m,c)$.

Analisi nel baricentro

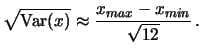
Osservando le formule (41) e (42) si nota che, se $\overline{x}$ è uguale a zero, il coefficiente di correlazione si annulla e anche l'espressione di $\sigma(c)$ è uguale a $\sigma_r/\sqrt{n}$. Questo suggerisce che per semplificare i conti conviene scegliere l'asse delle ascisse in corrispondenza del baricentro dei punti, ovvero effettuare la trasformazione di variabili

$$x^\prime = x - \overline{x}\,;$$

questo è particolarmente comodo se successivamente si deve utilizzare la retta trovata per delle estrapolazioni o, in generale, come curva di taratura. Chiaramente si otterrano in questo caso valori $m^\prime$ e $c^\prime$ diversi da $m$ e da $c$ ed è facile dimostrare che $c^\prime$ è uguale al baricentro delle $\overline{y}$.

Se si vuole visualizzare l'incertezza su $m^\prime$ e su $c^\prime$ sarà sufficiente

• tracciare le rette passanti per il baricentro e di pendenze $m^\prime\pm\sigma(m^\prime)$;
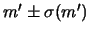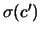• disegnare una barra verticale centrata nel baricentro e di semiampiezza $\sigma(c^\prime)$.

E' possibile passare poi dai parametri nel sistema del centro di massa a quelli nel sistema originale tenendo conto che $m\pm\sigma(m) = m^\prime\pm\sigma(m^\prime)$, $c = c^\prime -\overline{x}\, m$ e valutando $\sigma(c)$ e $\rho(m,c)$ dalle (41) e (42).