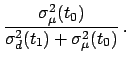Next: Binomial model
Up: Inferring numerical values of
Previous: Bayesian inference on uncertain
Gaussian model
Let us start with a classical example in which the response signal  from a detector is described by a Gaussian error function
around the true value
from a detector is described by a Gaussian error function
around the true value  with a standard deviation
with a standard deviation  ,
which is assumed to be exactly known.
This model is the best-known among physicists and, indeed,
the Gaussian pdf is also known as normal because
it is often assumed that
errors are 'normally' distributed according to this function.
Applying Bayes' theorem for continuous variables
(see Tab. 1), from the likelihood
,
which is assumed to be exactly known.
This model is the best-known among physicists and, indeed,
the Gaussian pdf is also known as normal because
it is often assumed that
errors are 'normally' distributed according to this function.
Applying Bayes' theorem for continuous variables
(see Tab. 1), from the likelihood
we get for 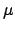
Considering all values of 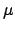 equally likely over a very large
interval, we can model the prior
equally likely over a very large
interval, we can model the prior 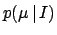 with
a constant, which simplifies in Eq. (26),
yielding
with
a constant, which simplifies in Eq. (26),
yielding
Expectation and standard deviation of the posterior
distribution are
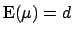 and
and
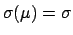 , respectively.
This particular result
corresponds to what is often done intuitively in practice. But
one has to pay attention to the assumed conditions under which the result
is logically valid: Gaussian likelihood and uniform prior.
Moreover, we can speak about the probability of true values only
in the subjective sense. It is recognized that physicists, and scientists
in general, are highly confused about this point (D'Agostini 1999a).
, respectively.
This particular result
corresponds to what is often done intuitively in practice. But
one has to pay attention to the assumed conditions under which the result
is logically valid: Gaussian likelihood and uniform prior.
Moreover, we can speak about the probability of true values only
in the subjective sense. It is recognized that physicists, and scientists
in general, are highly confused about this point (D'Agostini 1999a).
A noteworthy case of a prior for which the naive inversion
gives paradoxical results is when the value of a quantity is constrained
to be in the `physical region,' for example 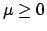 ,
while
,
while 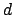 falls outside it (or it is at its edge).
The simplest prior that cures the problem
is a step function
falls outside it (or it is at its edge).
The simplest prior that cures the problem
is a step function
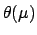 ,
and the result is
equivalent to simply renormalizing the pdf in the physical region
(this result corresponds to a `prescription' sometimes used by
practitioners with a frequentist background when they encounter
this kind of problem).
,
and the result is
equivalent to simply renormalizing the pdf in the physical region
(this result corresponds to a `prescription' sometimes used by
practitioners with a frequentist background when they encounter
this kind of problem).
Another interesting case is when the prior knowledge can be
modeled with a Gaussian function, for example, describing our
knowledge from a previous inference
Inserting Eq. (28) into
Eq. (26), we get
where
We can then see that the
case
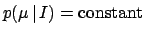 corresponds
to the limit of a Gaussian prior
with very large
corresponds
to the limit of a Gaussian prior
with very large 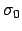 and finite
and finite 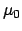 .
The formula for the expected value combining
previous knowledge and present experimental information
has been written in several ways in Eq.(31).
.
The formula for the expected value combining
previous knowledge and present experimental information
has been written in several ways in Eq.(31).
Another enlighting way of writing Eq.(30) is
considering 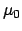 and
and 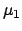 the estimates of
the estimates of 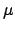 at times
at times 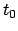 and
and 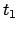 , respectively
before and after the observation
, respectively
before and after the observation 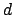 happened at time
happened at time 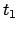 .
Indicating the estimates at different times by
.
Indicating the estimates at different times by 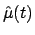 ,
we can rewrite Eq.(30) as
,
we can rewrite Eq.(30) as
where
Indeed, we have given Eq.(30) the structure of a
Kalman filter (Kalman 1960). The new observation `corrects' the
estimate by a quantity given by the innovation (or residual)
![$ [d(t_1) - \hat\mu(t_0)]$](img180.png) times the blending factor (or gain)
times the blending factor (or gain)
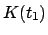 . For an introduction about Kalman filter and its probabilistic
origin, see (Maybeck 1979 and Welch and Bishop 2002).
. For an introduction about Kalman filter and its probabilistic
origin, see (Maybeck 1979 and Welch and Bishop 2002).
As Eqs. (31)-(35) show, a new experimental
information reduces the uncertainty. But this is true as long
the previous information and the observation are somewhat consistent.
If we are, for several reasons, sceptical about the model which yields
the combination rule (31)-(32),
we need to remodel the problem and introduce possible
systematic errors or underestimations of the quoted standard deviations,
as done e.g. in (Press 1997, Dose and von der Linden 1999,
D'Agostini 1999b, Fröhner 2000).



Next: Binomial model
Up: Inferring numerical values of
Previous: Bayesian inference on uncertain
Giulio D'Agostini
2003-05-13
![$\displaystyle \frac{1}{\sqrt{2\pi}\,\sigma}\exp\left[
-\frac{(d-\mu)^2}{2\,\sigma^2}\right]$](img147.png)
![]() ,
while
,
while ![]() falls outside it (or it is at its edge).
The simplest prior that cures the problem
is a step function
falls outside it (or it is at its edge).
The simplest prior that cures the problem
is a step function
![]() ,
and the result is
equivalent to simply renormalizing the pdf in the physical region
(this result corresponds to a `prescription' sometimes used by
practitioners with a frequentist background when they encounter
this kind of problem).
,
and the result is
equivalent to simply renormalizing the pdf in the physical region
(this result corresponds to a `prescription' sometimes used by
practitioners with a frequentist background when they encounter
this kind of problem).
![]() and
and ![]() the estimates of
the estimates of ![]() at times
at times ![]() and
and ![]() , respectively
before and after the observation
, respectively
before and after the observation ![]() happened at time
happened at time ![]() .
Indicating the estimates at different times by
.
Indicating the estimates at different times by ![]() ,
we can rewrite Eq.(30) as
,
we can rewrite Eq.(30) as