Esercizio 53 - Esercizio 54 - Esercizio 55 - Esercizio 56 - Esercizio 57 - Esercizio 58 - Esercizio 59 - Esercizio 60 - Esercizio 61
Esercizio 53

Una spira quadrata rigida, di lato $l = 12$ cm e resistenza $R = 25\, \Omega$, viene trascinata con velocità orizzontale costante, $v=3$ m/s. La spira entra in una zona di larghezza $d = 2l$ in cui è presente un campo magnetico $B = 4.5$ T ortogonale alla spira ed uscente dal piano del disegno. Determinare:
il verso della corrente indotta nella spira nelle varie fasi del moto;
in quali regioni agisce una forza sulla spira, il suo verso e la sua intensità;
l’energia totale dissipata nella resistenza dopo che la spira è completamente uscita dalla zona con campo magnetico;
la carica che globalmente ha fluito lungo la spira.
Soluzione
La corrente scorrerà solo in quelle regioni di spazio nelle quali il flusso del campo magnetico attraverso la spira sta variando. Questo avviene quando la spira entra ed esce dalla regione di campo. Per la legge di Lenz la corrente che scorre in un conduttore per effetto dell’induzione elettromagnetica si oppone sempre alla variazione di flusso. Quando la spira entra nella regione in cui è presente il campo, il flusso aumenta e quindi la corrente deve essere tale da generare un campo magnetico che si opponga al campo già presente. Considerando che il campo è uscente, la corrente dovrà quindi scorrere in senso orario per generare un campo entrante. Quando la spira esce, il flusso diminuisce e quindi la corrente dovrà scorrere in senso antiorario, così da generare un campo parallelo a quello presente, tendendo così a contrastare la variazione di flusso. L’intensità della corrente è in entrambi i casi $$ i = \frac{\mathcal{E}_i}{R} = \frac{l B v}{R} $$
Ragionando come sopra, la forza agisce solo quando vi è una variazione di flusso, quindi quando la spira entra ed esce dalla regione in cui è presente il campo. Quando la spira entra, la forza sul lato di destra non è bilanciata dal lato opposto (che non sente ancora l’effetto del campo magnetico) e quindi la spira sentirà una forza magnetica $$ \vec{F} = i\vec{l} \times \vec{B}. $$ Poiché la corrente scorre in verso orario (vedi sopra), in quel lato $\vec{l}$ è diretto verso il basso, e quindi la forza risultante varrà $$ \vec{F} = - \frac{l^2 B^2 \vec{v}}{R} $$ che ha modulo $F = 35$ mN. Quando la spira esce, solo il lato di sinistra risente del campo magnetico. Ragionando come sopra, ma considerando che ora la corrente scorre in verso antiorario, si trova di nuovo $$ \vec{F} = - \frac{l^2 B^2 \vec{v}}{R} $$ che quindi ha stessi modulo, direzione e verso di prima.
In generale il lavoro è dato da $$ W = \int_s \vec{F} \cdot d\vec{s}, $$ dove $s$ è lo spostamento fatto. in questo caso l’espressione della forza è quella trovata precedentemente, che è costante quando diversa da 0, mentre lo spostamento è nella direzione del moto, quindi antiparallelo alla forza stessa. $F$ è diversa da 0 unicamente quando la spira entra ed esce dalla regione di campo, e questo avviene per una lunghezza $l$ in entrambi i casi. Lo spostamento totale è quindi $s = 2l$, quindi il lavoro vale $$ W = - 2 F l = -8.4\, {\rm mJ} $$
Abbiamo visto a lezione che la carica totale che passa in una spira per effetto dell’induzione elettromagnetica è legata alla differenza di flusso del campo: $$ q = \int_{t_1}^{t_2} dq = \int_{t_1}^{t_2} i(t) dt = -\frac{1}{R} \int_{t_1}^{t_2} d\Phi = \frac{\Phi_1 - \Phi_2}{R}. $$ Poiché in questo caso $\Phi_1 = \Phi_2 = 0$, dato che la spira è fuori dalla regione in cui è presente il campo magnetico sia all’inizio che alla fine del moto, $q = 0$. Questo avviene perché quando la spira entra nella regione di campo la corrente scorre in un verso, trasportando una certa quantità di carica $\Delta q$, mentre quando la spira esce la corrente scorre nel verso opporto, trasportando di nuovo $\Delta q$. La somma di questi due contributi, se teniamo conto del verso opposto, è nulla.
Esercizio 54
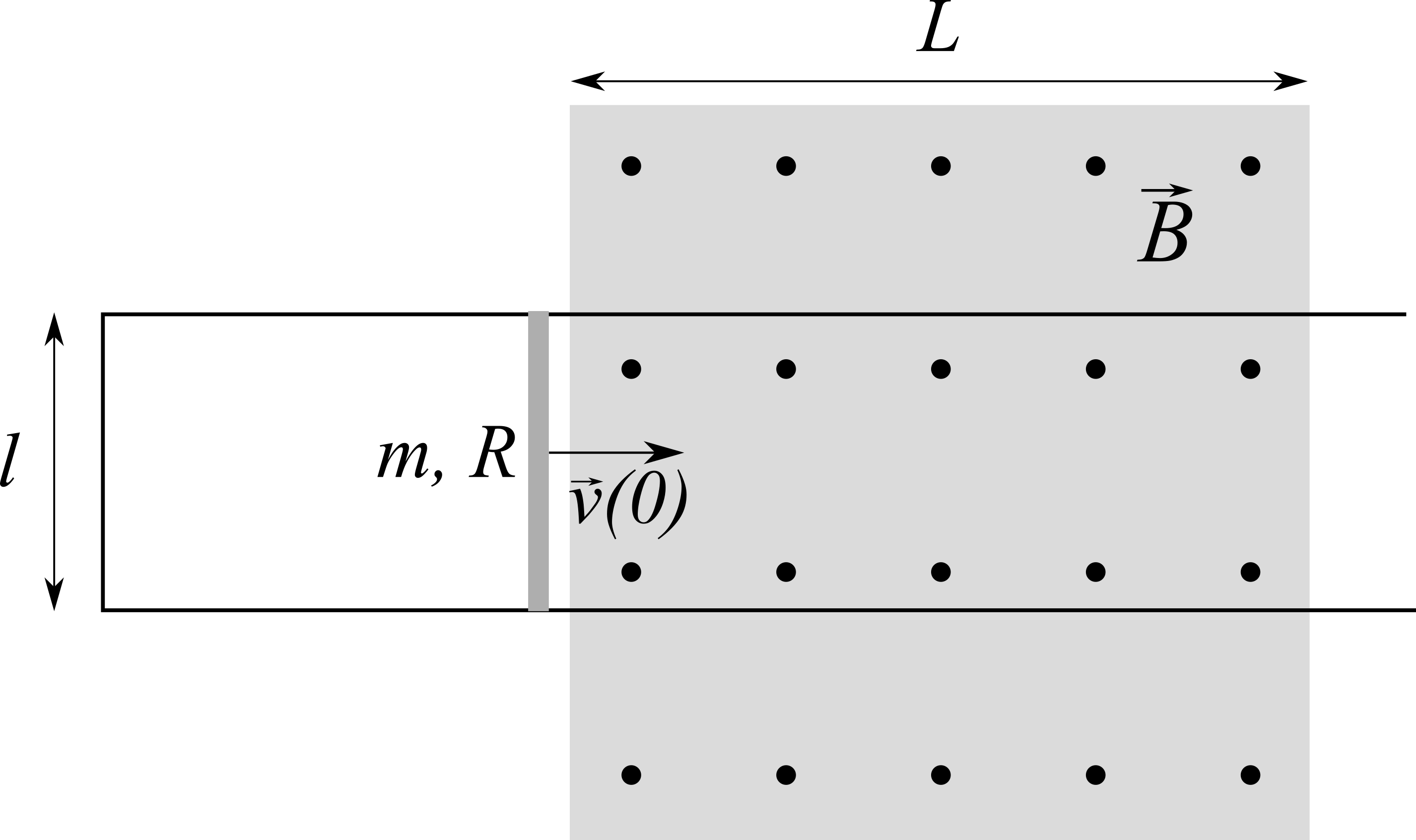
Una sbarretta conduttrice di massa $m=5$ g e di lunghezza $l=25$ cm scorre liberamente su due binari orizzontali ai quali è elettricamente connessa. I due binari sono connessi tra di loro da una resistenza $R=15\, \Omega$. Per un tratto di lunghezza $L=40$ cm i binari sono attraversati da un campo magnetico uniforme $B=2.5$ T diretto verticalmente ed uscente dal foglio (vedi disegno). La sbarretta arriva al tempo $t=0$ nella zona con campo magnetico con una velocità $v(0)=2.5$ m/s. Determinare
il verso e l’intensità della corrente che fluisce nella barretta a $t = 0$;
la carica fluita nel circuito sbarretta-rotaie-resistenza dopo che la sbarretta è uscita dalla zona con campo magnetico;
la velocità di uscita della barretta;
la dimensione della regione di campo che si dovrebbe avere per far fermare completamente la sbarretta.
Soluzione
La corrente deve opporsi all’aumentare del flusso, e quindi, dovendo generare un campo opposto a $B$, scorrerà in verso orario. L’intensità della corrente si trova applicando la legge di Faraday, ricordando che il flusso è $$ \Phi(B) = lBx(t) $$ e quindi $$ \mathcal{E}_i(t) = - \frac{d \Phi(B)}{dt} = -l B v(t) $$ che calcolata in 0 vale $\mathcal{E}_i(0) = -l B v(0)$, da cui si ricava $$ i = \frac{l b v(0)}{R} = 0.104\, {\rm A} $$
La variazione di flusso a cui è sottoposta la spira è semplicemente $$ \Delta \Phi = \Phi_1 - \Phi_2 = -\Phi_2 = -lLB $$ e quindi la carica è data dalla legge di Felici: $$ q = \frac{\Delta \Phi}{R} = -0.017 \, {\rm C}. $$
In questo caso la velocità con cui si muove la sbarretta non è costante poiché comincerà a rallentare non appena entrata nella regione di campo come conseguenza della presenza della forza di attrito elettromagnetico data da $$ F(t) = - \frac{l^2 B^2}{R}v(t) $$ dove omettiamo i simboli di vettore perché forza e velocità sono sempre parallele. Ricordando che $v(t) = dx / dt$ e $a(t) = F(t) / m$ e definendo $t_u$ come il tempo a cui la sbarrretta esce dalla regione di campo possiamo risolvere direttamente l’equazione che lega accelerazione a velocità: $$ v(t_u) = v(0) + \int_0^{t_u} a(t) dt = v(0) - \int_0^{t_u} \frac{l^2 B^2}{mR} v(t) dt = v(0) - \int_0^{t_u} \frac{l^2 B^2}{mR}\frac{dx}{dt} dt = v(0) - \int_0^L \frac{l^2 B^2}{mR} dx $$ che si può risolvere immediatamente per ottenere $$ v(t) = v(0) - \frac{l^2 B^2 L}{mR} = 0.42\, {\rm m/s} $$
Far fermare la sbarretta significa imporre $v(t) = 0$. Sostituendo questo valore nell’equazione precedente si trova $$ L = \frac{v(0) mR }{l^2 B^2} = 0.48\, {m} $$
Esercizio 55

In un piano inclinato di angolo $\theta=\pi / 6 = 30^\circ$ sono poste due rotaie parallele, distanti $l=10$ cm, di resistenza elettrica trascurabile e connesse elettricamente tra loro alla sommità. Su di esse può scorrere senza attrito una sbarretta conduttrice di massa $m=10$ g e resistenza elettrica $R=0.1\, \Omega$. Il tutto è immerso in un campo magnetico uniforme e costante, diretto verticalmente, di modulo $B=0.5$ T. Ad un certo istante la sbarretta viene lasciata libera di scivolare lungo il piano inclinato. Determinare:
verso e intensità della corrente indotta nella spira individuata dal sistema rotaie-sbarretta in funzione della velocità della sbarretta.
la velocità limite della sbarretta nel suo moto di scivolamento.
Soluzione
Il verso è dato dalla legge di Lenz: poiché il flusso attraverso la spira aumenta, il campo magnetico generato dalla corrente indotta deve opporsi a quello esterno e quindi, nel sistema di riferimento indicato in figura, la corrente scorre lungo $-\hat{z}$ all’interno della sbarretta. Possiamo ricavare la corrente a partire dalla legge di Faraday. Il flusso del campo attraverso la superficie della spira è $$ \Phi(B) = l x B \cos \theta $$ perché tra la normale alla spira e il campo magnetico vi è un angolo $\theta$. $x$ indica lo spostamento della sbarretta lungo il piano parallelo rispetto alla sua posizione iniziale. La forza elettromotrice indotta sarà quindi $$ \mathcal{E}_i = -\frac{d \Phi(B)}{dt} = - l B \cos \theta v(t) $$ perché $dx / dt = v(t)$, quindi la corrente ha intensità $$ i = \frac{l B \cos \theta v(t)}{R} $$
La velocità limite si raggiunge quando $v$ rimane costante durante il moto. Affinché la velocità sia costante l’accelerazione deve essere nulla, e quindi la somma delle forze deve anch’essa azzerarsi. Le componenti ortogonali al piano si azzerano in forza della reazione normale. Le componenti parallele, d’altro canto, devono azzerarsi perché uguali in modulo ma opposte in verso. Col sistema di riferimento indicato in figura la forza peso ha direzione $-\hat{y}$, mentre quella magnetica vale
$$ \vec{F}_m = i \vec{l} \times \vec{B} = \frac{l^2 B^2}{R} \cos \theta v(t) \hat{x} $$
poiché la corrente scorre nella sbarretta verso $\hat{z}$ e $\vec{B}$ è diretto lungo $\hat{y}$. Eguagliando le intensità delle componenti delle due forze lungo il piano inclinato si trova $$ mg \sin\theta = \frac{l^2 B^2}{R} \cos^2 \theta v_{\rm lim} $$ da cui si ricava $$ v_{\rm lim} = \frac{mg R \tan \theta}{l^2 B^2 \cos \theta} $$
Esercizio 56

Una bobina rettangolare formata da $N = 100$ spire sovrapposte di lati $a = 1$ cm e $b = 5$ cm è collegata a dei collettori circolari e ruota intorno all’asse che passa per i lati corti con velocità angolare $\omega$ all’interno di una regione in cui è presente un campo magnetico uniforme $B = 0.4$ T.
Ricavare l’espressione del flusso quando la bobina si trova nella posizione in figura (cioè quando $B$ è ortogonale al piano della spira)
Determinare l’espressione della differenza di potenziale massima tra i collettori, specificando per quale posizione della bobina valga.
Calcolare a quale velocità angolare la bobina deve ruotare per ottenere una differenza di potenziale massima pari a 100 V.
Soluzione
Nella posizione data il campo e la normale alla bobina sono paralleli, quindi il flusso è la somma dei flussi che passano attraverso le $N$ spire, quindi $$ \Phi(B) = N a b B = 0.02\, {\rm Wb} $$
Se definiamo $\theta = \omega t$ l’angolo tra la normale alla bobina e il campo, il flusso vale $$ \Phi(B) = N a b B \cos \theta = N a b B \cos (\omega t) $$ e quindi applicando la legge di Faraday troviamo $$ \mathcal{E}_i = \omega N a b B \sin(\omega t) $$ che è massimo quando $\theta = \omega t = \pi / 2$, cioè quando campo e bobina sono ortogonali.
Utilizzando la formula di prima e imponendo $\mathcal{E}_i = 100$ V troviamo $$ \omega = \frac{\mathcal{E}_i}{N a b B} = 5000 \, {\rm rad/sec} $$
Esercizio 57
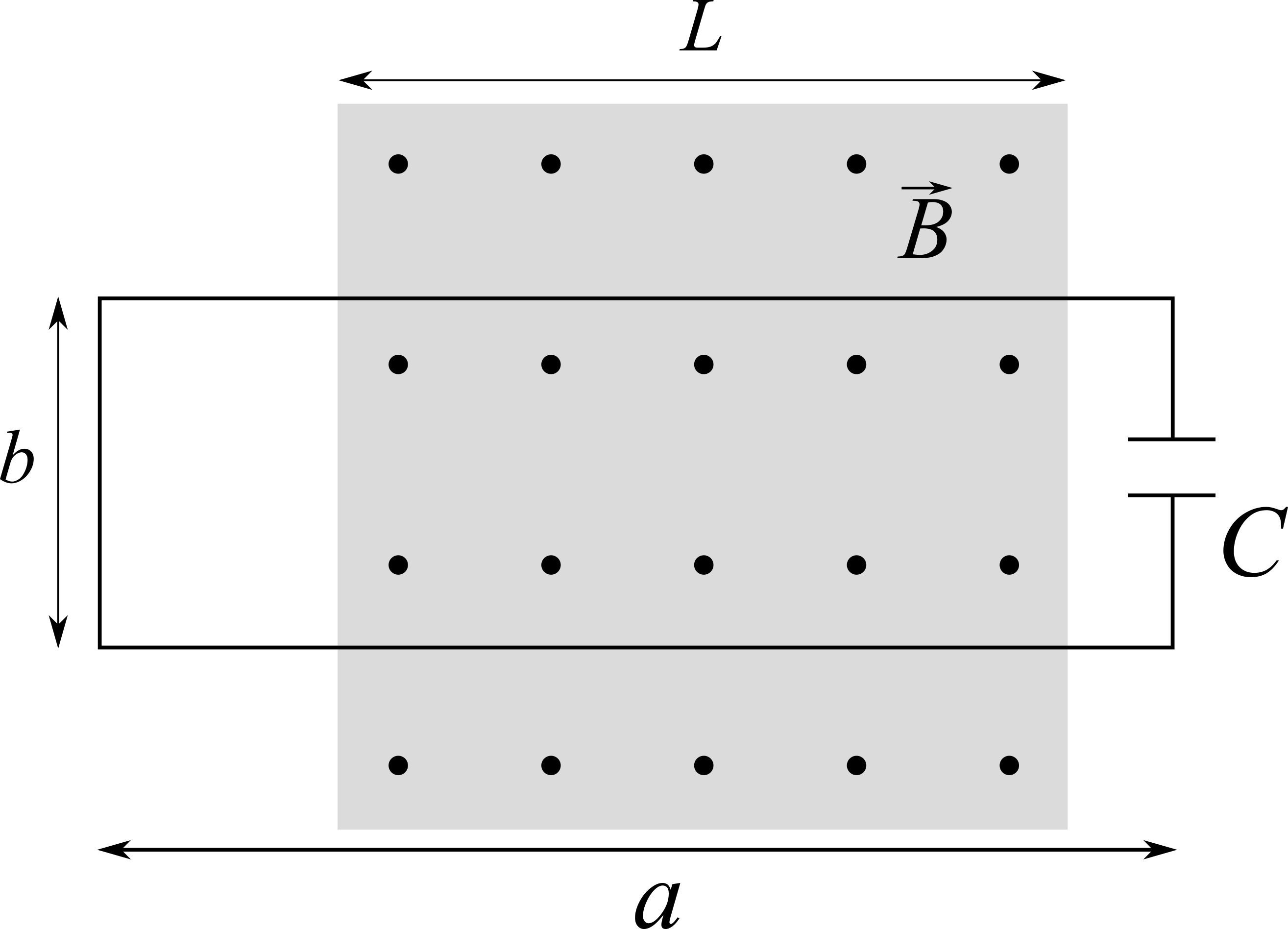
Un circuito chiuso di forma rettangolare di dimensioni $a$ cm e $b$ cm contenente un condensatore di capacità $C$ è parzialmente immerso in una regione di campo magnetico larga $L$ cm (vedi disegno). Il campo magnetico ha direzione e verso ortogonale al circuito e modulo che varia nel tempo con la legge $B(t) = B_0 \exp(-t / \tau)$. Determinare segno e quantità di carica $q(t)$ presente sulle armature del condensatore.
Soluzione
Applichiamo la legge di Faraday utilizzando come cammino il circuito percorso in senso antiorario, così che la normale alla superficie sia parallela al campo magnetico. Il flusso del campo attraverso questa superficie è
$$ \Phi(B) = B_0 b L \exp(-t / \tau) $$
e quindi la forza elettromotrice indotta vale
$$ \mathcal{E}_i = -\frac{d\Phi(B)}{dt} = \frac{B_0 b L \exp(-t / \tau)}{\tau}. $$
La f.e.m. è positiva e quindi coerente con il verso scelto antiorario scelto. Come conseguenza, il condensatore avrà l’armatura superiore carica negativamente e quella inferiore carica positivamente. La differenza di potenziale ai capi delle armature non può che essere la f.e.m. indotta, quindi la carica varrà
$$ q(t) = C \mathcal{E}_i = \frac{C B_0 b L \exp(-t / \tau)}{\tau}. $$
Esercizio 58
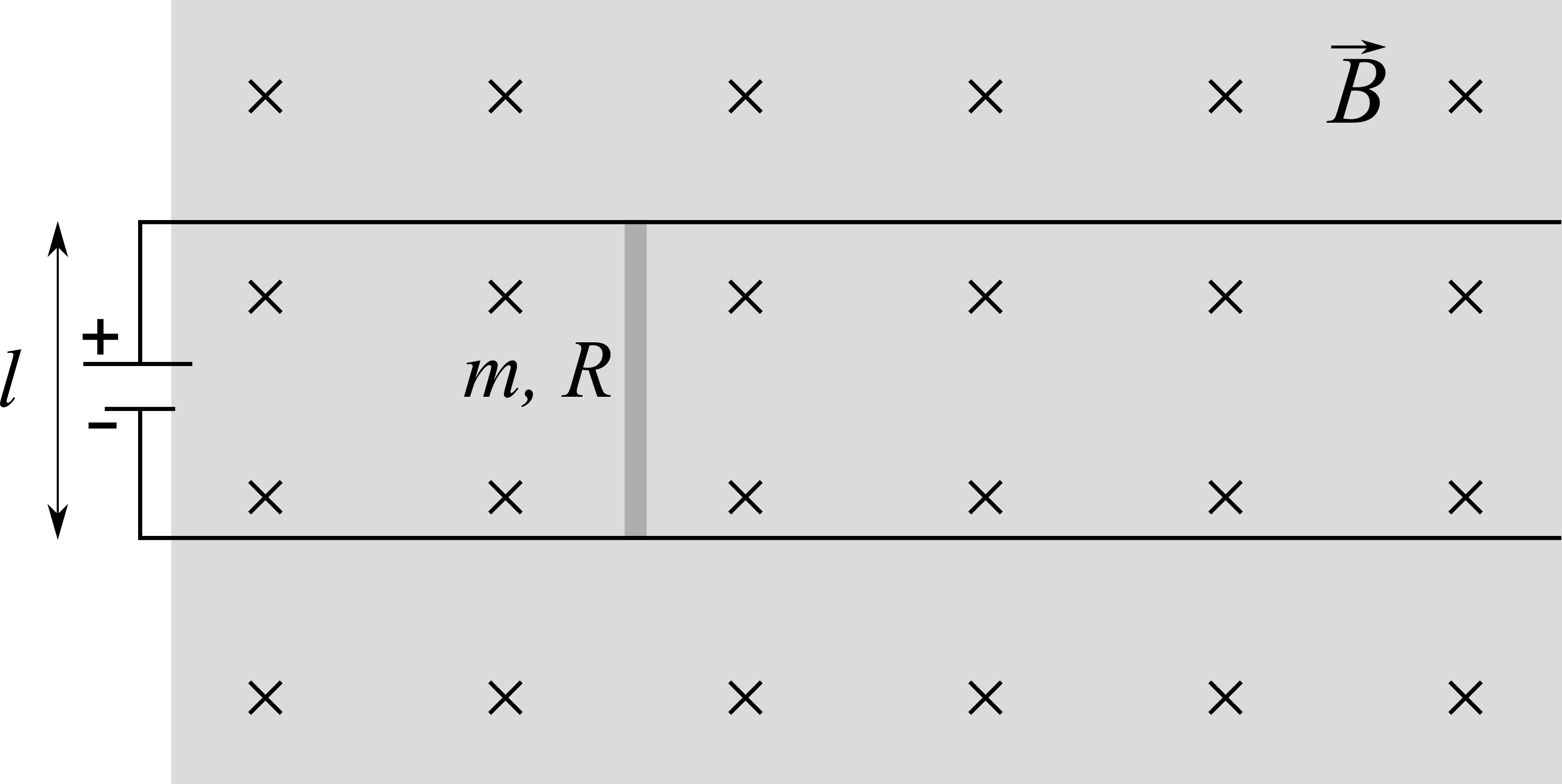
Una barra conduttrice, di massa $m=100$ g e resistenza $R = 500\, \Omega$, appoggia senza attrito su due binari orizzontali di resistenza trascurabile. La distanza tra i binari è $l=40$ cm e il sistema è immerso in un campo magnetico uniforme $B=0.8$T, perpendicolare ai binari ed alla barra (entrante nel foglio, vedi figura). All’istante $t=0$ la barra è ferma e tra i binari viene posto un generatore con la polarità indicata in figura.
-
Se il generatore fornisce una corrente costante $i_0 = 0.2$ A calcolare:
in che direzione si muove la sbarra;
la velocità della sbarra al tempo $t_1=15$ s;
il lavoro fatto dal generatore fino al tempo $t_1$.
-
Se invece il generatore fornisce una f.e.m. costante pari a $\mathcal{E}_0= 8$ V calcolare
la potenza fornita dal generatore quando la sbarra ha raggiunto la velocità limite;
il valore della velocità limite.
Soluzione
-
Poiché nella sbarretta scorre una corrente costante $i_0$, essa sarà soggetta ad una forza (anch’essa costante) data da $$ \vec{F} = i_0 \vec{l} \times \vec{B} $$ che, dati i versi indicati in figura, ha direzione verso destra.
Poiché la sbarretta parte da ferma, la sua velocità sarà parallela alla forza, e quindi si muoverà verso destra.
Ricordando che $\vec{F} = m \vec{a}$ troviamo subito che $$ v(t) = at = \frac{i_0lBt}{m} $$ che per $t_1 = 15$ s vale $v(t_1) = 9.6$ m/s.
All’inizio del moto la sbarretta è ferma e la f.e.m. totale ai capi del circuito è $\mathcal{E}_0 = R i_0$. Quando la sbarretta si mette in moto, a questa f.e.m. va sommata a quella indotta che si oppone alla sorgente di moto. Considerando che il flusso è $\Phi(B) = x(t) l B$ (vedi esercizi precedenti) la f.e.m. indotta vale $$ \mathcal{E}_i = - \frac{d\Phi}{dt} = - \frac{dx}{dt} l B = - v(t) l B = - \frac{i_0l^2B^2t}{m} $$ Poiché la corrente deve rimanere costante, la f.e.m. nel circuito deve anche rimanere costante (perché la resistenza non varia), e quindi la f.e.m. che il generatore eroga, dovendo contrastare $\mathcal{E}_i$, sarà $$ \mathcal{E}(t) = \mathcal{E}_0 - \mathcal{E}_i = Ri_0 + v(t) l B = Ri + \frac{i_0l^2B^2t}{m} $$ Ricordando il legame tra potenza, differenza di potenziale e corrente si trova $$ \mathcal{P} = \mathcal{E}(t) i_0 = Ri_0^2 + \frac{i_0^2l^2B^2t}{m} $$ che integrata da 0 a $t_1$ dà proprio l’energia dissipata: $$ W = Ri_0^2 t_1 + \int_0^{t_1} \frac{i_0^2l^2B^2t}{m} dt = Ri_0^2 t_1 + \frac{1}{2} \frac{i_0^2l^2B^2t_1^2}{m}. $$ Questo risultato si poteva trovare anche considerando che l’energia fornita dal generatore viene parzialmente trasformata in energia cinetica, e quindi l’energia totale erogata si può scrivere come $$ W = Ri_0^2 + \frac{1}{2}m v(t)^2 $$ che dà lo stesso risultato (provate!).
-
Se la tensione (invece della corrente) è costante il comportamento del sistema cambia qualitativamente, poiché la f.e.m. indotta genererà una corrente che non verrà più contrastata dall’aumento della f.e.m. erogata dal generatore. Definiamo $i$ la corrente erogata dal generatore e $i_i$ quella dovuta alla presenza della f.e.m. indotta.
Se un oggetto raggiunge una velocità limite significa che la risultante delle forze agenti su di esso è nulla. L’unica forza che può agire sulla sbarra è quella magnetica $i \vec{l} \times \vec{B}$. L’unico modo affinché sia zero è che sia nulla la corrente che scorre attraverso la sbarra, cioè si deve avere $i = i_i$ (perché le due correnti scorrono in verso opposto). Se è nulla la corrente, sarà nulla anche la potenza erogata.
Poiché $\mathcal{E}_0$ è costante, si avrà $$ i = \frac{\mathcal{E}_0}{R}, $$ mentre la corrente indotta si trova tramite la legge di Faraday, $$ i_i = \frac{\mathcal{E}_i}{R} = \frac{l B v}{R}. $$ Uguagliando le due correnti si ottiene $$ v = \frac{\mathcal{E}_0}{l B} = 25\, {\rm m/s} $$
Esercizio 59
Un circuito è composto da una batteria di f.e.m. $\mathcal{E}$, da una resistenza $R = 0.1 \, \Omega$, da un’induttanza ($L = 9.44$ H) e da un interruttore, inizialmente chiuso. Al tempo zero l’interruttore viene aperto. Sapendo che nei primi $15$ s la corrente passa da $1.16$ A a $10.2$ mA. Determinare
il valore di $\mathcal{E}$;
il valore della resistenza $R’$ presente tra i due poli dell’interruttore.
Soluzione
La legge oraria con cui varia l’intensità di corrente in un circuito $RL$ che viene scollegato dal generatore è $$ i(t) = i_{\infty} e^{-\frac{t}{\tau}}, $$ dove $i_{\infty} = \frac{\mathcal{E}}{R}$ è il valore della corrente a circuito chiuso e $\tau = L / R’$. Dal testo si capisce che $i_{\infty} = 1.16$ A e $i(15 \, {\rm s}) = 10.2$ mA. Utilizzando la prima relazione si trova $$ \mathcal{E} = R i_{\infty} = 0.116 \, {\rm V}. $$
Sapendo che $i(15 \, {\rm s}) = 10.2$ mA e risolvendo per $R’$ si trova $$ R’ = \frac{L}{15 \, {\rm s}} \log \left( \frac{i_{\infty}}{i(15 \, {\rm s})} \right) = 2.98 \, \Omega $$
Esercizio 60
Un induttore ($L=4 \times 10^{-4}$ H) ed una resistenza ($R=5\, \Omega$) sono posti in serie ad un generatore di tensione ($\mathcal{E} = 200$ V) collegato tramite un interruttore, inizialmente aperto. Al tempo zero l’interruttore viene chiuso. Determinare
il tempo che occorre affinché la corrente che fluisce nella resistenza raggiunga il 60% della corrente finale;
l’energia accumulata nel campo magnetico dopo che la corrente ha raggiunto il suo valore massimo;
il valore della corrente dopo un tempo pari a 3 costanti di tempo $\tau = L / R$.
Soluzione
La corrente finale è data dalla legge di Ohm e vale $$ i_{\infty} = \frac{\mathcal{E}}{R} = 40\, {\rm A}. $$ Sapendo che la corrente varia con la legge temporale $$ i(t) = \frac{\mathcal{E}}{R} \left( 1 - e^{-\frac{t}{\tau}}\right), $$ il tempo si trova imponendo $i(t) = 0.6 i_{\infty}$ e risolvendo per $t$: $$ t = - \frac{L}{R}\log(1 - 0.6) = 7.2 \times 10^{-6} \, {\rm s} $$
L’energia è data dalla relazione $$ U = \frac{1}{2} L i_{\infty}^2 = 0.32 \, {\rm J} $$
Il valore si ottiene sostituendo $t = 3 L / R$ in $i(t)$, trovando
$$ i(3 L / R) = 38\, {\rm A} $$
Esercizio 61
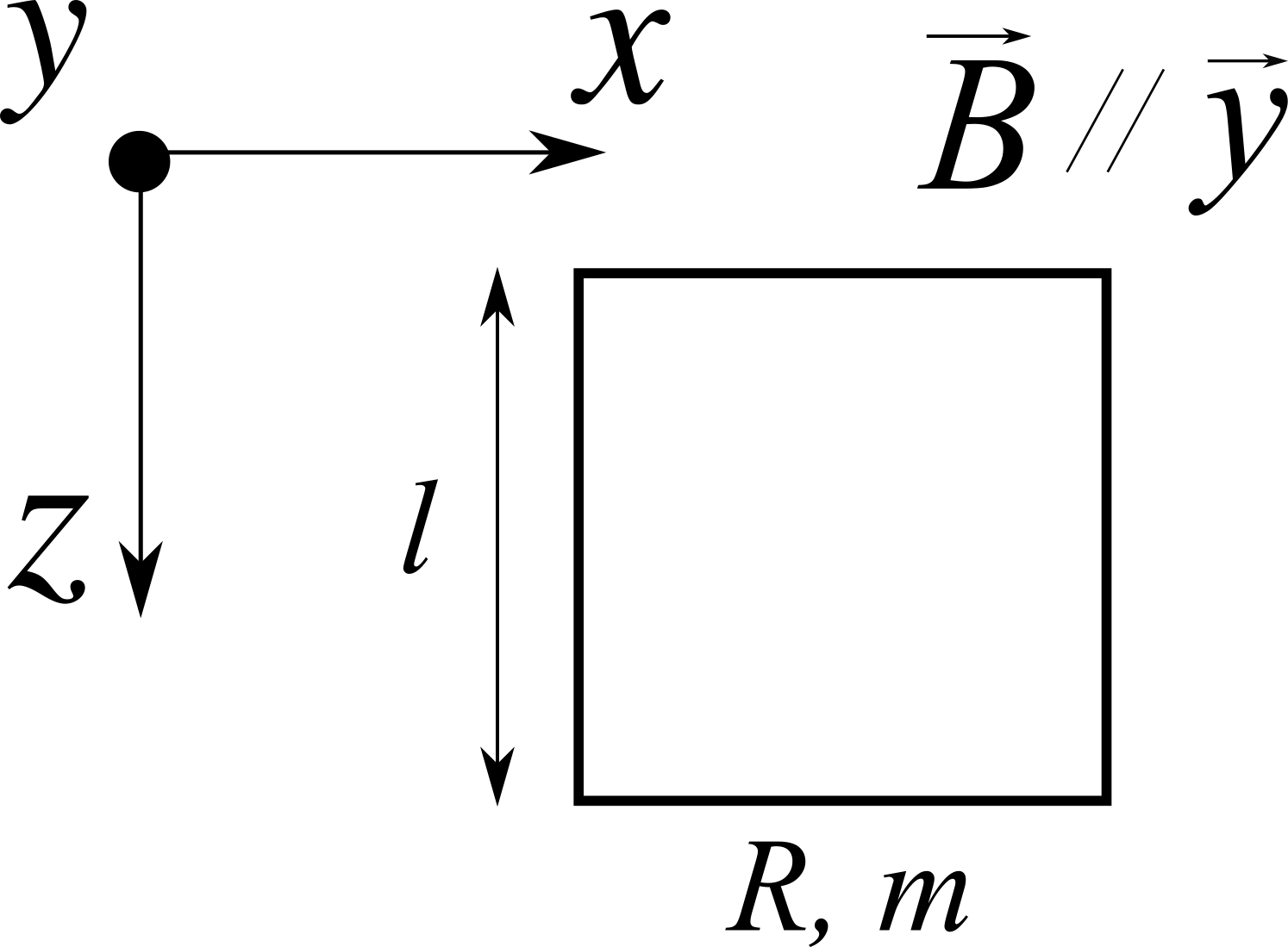
Una spira quadrata di resistenza $R = 10^{-3}\, \Omega$, massa $m = 10$ g e lato $l = 20$ cm viene lasciata cadere in una regione in cui è presente un campo di magnetico diretto lungo $\hat{y}$ avente modulo dipende dalla coordinata $z$: $$ B_y(z) = b z $$ con $b = 2 T / m$. La spira è orientata in maniera tale da avere normale parallela a $\vec{B}$.
Determinare intensità e verso della corrente indotta nella spira dal moto.
Determinare il valore della velocità limite $v_{\rm lim}$, trascurando l’autoinduzione della spira.
Calcolare la corrente che circola nella spira per $v = v_{\rm lim}$.
Soluzione
La corrente si calcola a partire dalla legge di Faraday. Per calcolare il flusso del campo, definiamo $h(t)$ la coordinata $z$ del lato più in alto della spira. Il flusso vale quindi $$ \Phi(B) = b\int_0^l dx \int_{h(t)}^{h(t) + l} z dz = l b\int_{h(t)}^{h(t) + l} z dz = l^2 b h(t) + \frac{1}{2} b l^3. $$ Poiché solo il primo termine dipende dal tempo, la f.e.m. indotta vale $$ \mathcal{E}_i = - l^2 b v(t) $$ dove $v(t)$ è la velocità della spira al tempo $t$. Il segno negativo indica che la f.e.m. genererà una corrente che, con la spira vista dalla prospettiva in cui $\hat{y}$ è uscente, scorre in senso orario. L’intensità varrà invece $$ i(t) = \frac{l^2 b v(t)}{R} $$
Ci sono tre forze agenti lungo $\hat{z}$: quella magnetica che agisce sul lato in alto, quella magnetica che agisce sul lato in basso e quella peso che agisce sul centro di massa della spira. Ricordando che la forza magnetica che agisce su di una porzione di filo in cui scorre corrente vale $\vec{F} = i \vec{l} \times \vec{B}$ si trova $$ F_{\rm tot} = \frac{l^3 b^2 v(t)}{R} h(t) - \frac{l^3 b^2 v(t)}{R} (h(t) + l) + mg = -\frac{l^4 b^2 v(t)}{R} + mg. $$ Quando la spira raggiunge la velocità limite si deve avere $F_{\rm tot} = 0$, da cui si ottiene $$ v_{\rm lim} = \frac{R mg}{l^4 b^2} = 0.015 \, {\rm m/s} $$
Sostituendo il valore della velocità limite ottenuto precedentemente si trova $$ i = \frac{l^2 b v_{\rm lim}}{R} = 1.2 \, {\rm A} $$