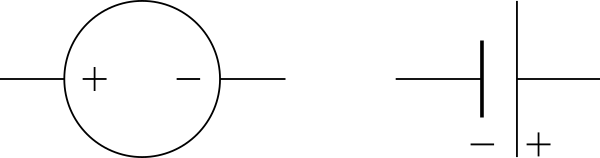
Modello classico della conduzione elettrica

MNV: paragrafi 5.4 e 5.2 (in questo ordine)

I portatori di carica (in questo caso elettroni) risentono dell’effetto del campo e si mettono in modo, generando una corrente elettrica. Data una superficie all’interno del conduttore, l’intensità media di questa corrente elettrica è definita come la quantità di carica $\Delta q$ che passa attraverso la superficie in un intervallo di tempo $\Delta t$:

$$ i_m = \frac{\Delta q}{\Delta t} $$

L’intensità di corrente istantanea è definita formalmente come il limite di $i_m$ per intervalli di tempo molto piccoli:

$$ i = \lim_{\Delta t \to 0} \frac{\Delta q}{\Delta t} = \frac{dq}{dt} $$

La corrente si misura in Ampere (A, che indica quanti Coulomb per secondo passano attraverso una data superficie).

Applichiamo ora il modello di Drude per trovare la relazione che lega la differenza di potenziale applicata ai capi del conduttore con la corrente che viene generata.

Senza prendere in considerazione effetti quantistici, consideriamo un conduttore solido come un “mare” di elettroni immersi in un reticolo di ioni. Il moto di ogni elettrone, che può essere modellizzato come rettilineo uniforme con velocità molto alta, $v \approx 10^6 $ m/s, viene interrotto di frequente dagli urti con gli ioni, che (con ottima approssimazione) ne randomizzano la direzione. La distanza percorsa tra un urto ed un altro è chiamato cammino libero medio $l$. Poiché la velocità è essenzialmente costante, il tempo che intercorre tra due urti vale:

$$ \tau_l = \frac{l}{v} $$

Senza campo elettrico, la media delle velocità degli elettroni vale $\frac{1}{N}\sum_i \vec{v}_i = 0$, perché non c’è passaggio netto di corrente. Se però il conduttore viene immerso in una regione di spazio in cui è presente un campo $\vec{E}$, ciascun elettrone avverte una forza $-e\vec{E}$, e quindi viene accelerato di $-e\vec{E}/m$. Se appena dopo un urto la velocità di un elettrone vale $\vec{v}_i^{(i)}$, poco prima dell’urto seguente (prima cioè che la velocità venga nuovamente randomizzata) si avrà:

$$ \vec{v}_i^{(f)} = \vec{v}_i^{(i)} - \frac{e\vec{E}}{m} \tau_l $$

Dove il fatto che $\tau_l$ non cambi per effetto del campo verrà giustificato a posteriori notando che le velocità in gioco (quella “naturale” degli elettroni e quella dovuta al campo) differiscono di molti ordini di grandezza. Se facciamo una media tra tutti gli elettroni, troviamo che la velocità non è più nulla ma ha valore finito che dipende dal campo e dalle proprietà degli elettroni:

$$ \vec{v}_d = \frac{1}{N}\sum_i \vec{v}_i^{(f)} = \frac{1}{N}\sum_i \vec{v}_i^{(i)} - \frac{e\vec{E}}{m} \tau_l = - \frac{e\vec{E}}{m} \tau_l $$

Dove $\vec{v}_d$ è detta velocità di deriva. Nota Bene: La media delle velocità iniziali viene nulla perché si ha, come vedremo fra poco, $v_d \ll v$, e quindi la distribuzione delle velocità per effetto degli urti resta casuale, indipendentemente da $\vec{E}$. In altre parole, l’effetto del campo viene “resettato” dopo ogni urto.

$\vec{v}_d$ è detta velocità di deriva perché è, in media, l’unica componente della velocità non nulla. Il suo effetto netto è quello di muovere gli elettroni lungo la direzione del campo. Stimiamo l’ordine di grandezza di $v_d$ sapendo che $l \sim 4 \times 10^{-8}$ m, $v = 10^6$ m/s, $e = -1.603 \times 10^{-19}$ C, $m = 9.1 \times 10^{-31}$ Kg e un campo elettrico tipico all’interno di un conduttore è dell’ordine di $10^{-2}$ V/m, quindi:

$$ v_d \approx 10^{-4}\, \mathrm{m / s} = 10^{-10} v $$

Il che dimostra (giustificando a posteriori le relazioni derivate sopra) come $v_d \ll v$.

Per mettere in relazione $i$ e $v_d$ prendiamo una superficie infinitesima all’interno del conduttore, $d\Sigma$, e calcoliamo la quantità di carica per unità di tempo che ci passa attraverso quando nel conduttore è presente un campo $\vec{E}$ che genera una velocità di deriva $\vec{v}_d \parallel \vec{E}$. Poiché, in generale, la normale $\hat{n}$ di $d\Sigma$ non è parallela ad $\vec{E}$ ma forma con esso un angolo $\theta$, mentre la velocità di deriva è costante, gli elettroni che attraversano $d\Sigma$ in un tempo $dt$ sono quelli contenuti nel cilindro obliquo di basi pari a $d\Sigma$ ed altezza pari a $v_d dt$. Disegnandolo si vede subito come il volume di questo solido sia

$$ d\tau = v_d\cos{\theta} d\Sigma dt $$

Moltiplicando questo valore per il numero medio di elettroni per unità di volume, cioè la densità numerica di elettroni che abbiamo chiamato $n$, si ottiene il numero di elettroni contenuti in $d\tau$ e che quindi passano attraverso $d\Sigma$. Poiché ogni elettrone ha carica $-e$ si trova

$$ dq = -n e v_d\cos{\theta} d\Sigma dt $$

e quindi

$$ di = \frac{dq}{dt} = -n e v_d\cos{\theta} d\Sigma $$

è l’intensità di corrente che passa attraverso $d\Sigma$. Se definiamo la densità di corrente come

$$ \vec{j} = -n e \vec{v}_d $$

la corrente attraverso $d\Sigma$ si può riscrivere come

$$ di = \vec{j} \cdot \hat{n} d\Sigma $$

Data una superficie finita $\Sigma$, l’intensità di corrente che passa attraverso di essa vale

$$ i = \int_{\Sigma} \vec{j} \cdot \hat{n} d\Sigma. $$

Che possiamo interpretare matematicamente come il flusso di $\vec{j}$ attraverso $\Sigma$. Se prendiamo una superficie ortogonale alla densità di corrente, si ottiene la relazione $i = j\Sigma$, e quindi

$$ j = \frac{i}{\Sigma} $$

da cui discende il nome di $\vec{j}$, che infatti può essere definita come l’intensità di corrente che passa attraverso l’unità di superficie ortogonale alla direzione del moto delle cariche.

Nel ricavare $\vec{j}$ abbiamo considerato portatori di carica negativi. In questo caso, se sostituiamo la relazione che lega $\vec{j}$ ad $\vec{E}$ ricavata precedentemente troviamo

$$ \vec{j} = -n e \vec{v}_d = \frac{ne^2\vec{E}}{m} \tau_l $$

La densità di corrente ed il campo sono quindi proporzionali. Questa relazione è nota come legge di Ohm della conduttività elettrica. Poiché $e^2 \tau_l / m$ è definito positivo, $\vec{j}$ ha sempre lo stesso verso del campo. Inoltre, la dipendenza dalla carica dei portatori è data dal termine $e^2$, e quindi lo stesso identico risultato è valido anche qualora i portatori fossero positivi. Il fatto che $\vec{j}$ ed $\vec{E}$ siano sempre concordi implica che non sia possibile misurare il segno dei portatori di carica eseguendo misure macroscopiche di corrente: gli effetti macroscopici di una data differenza di potenziale non dipendono dal segno della carica dei portatori. Nota Bene: data questa premessa, il verso della corrente (che si considera scorrere dal polo positivo, a potenziale maggiore, a quello negativo, a potenziale minore) è solamente una convenzione.

Potenza ed effetto Joule

Una carica in presenza di un campo elettrostatico accelera. Il lavoro della forza elettrostatica viene tramutato tutto in energia cinetica, che cresce continuamente a spese dell’energia potenziale. Nel caso degli elettroni nei conduttori la velocità di deriva è circa costante, anche in un campo uniforme (che dovrebbe indurre un’accelerazione costante). Dove va a finire il lavoro fatto dal campo elettrico se l’energia cinetica non varia? Viene dissipato in calore, che si sviluppa dalla resistenza che il reticolo del conduttore oppone al passaggio degli elettroni. Possiamo calcolare questo lavoro in un conduttore posto ad una d.d.p $\Delta V$:

$$ dW = \Delta V dq = \Delta V i dt $$

Il lavoro speso nell’unità di tempo si chiama potenza (in questo caso potenza elettrica):

$$ \mathcal{P} = \frac{dW}{dt} = \Delta V i = R i^2 = \frac{\Delta V^2}{R} $$

dove le ultime due relazioni sono valide se vale la legge di Ohm. La potenza si esprime in watt (W $=$ J / s). Possiamo quindi scrivere il lavoro compiuto dal campo in un tempo $t$ come

$$ W = \int_0^t \mathcal{P} dt’ = \int_0^t R i^2 dt’ $$

Se la corrente è costante nel tempo si ha $W = R i^2 t$. Il lavoro viene assorbito dal conduttore sotto forma di calore, provocando un aumento di temperatura. In generale, quindi, la temperatura di un conduttore percorso da corrente aumenta tanto più quanto l’intensità della corrente è grande. Questo aumento di temperatura, che prende il nome di effetto Joule, può persino portare alla fusione del materiale.

Esiste una classe di materiali che hanno resistività così piccola da essere essenzialmente zero: i cosiddetti superconduttori. Purtroppo l’effetto di superconduttività si osserva solo a temperature molto basse, e quindi le applicazioni di questi materiali sono limitate (ma comunque importanti: risonanze magnetiche, acceleratori di particelle).

Resistori in serie

Ora che abbiamo introdotto il concetto di corrente possiamo definire meglio cos’è un collegamento in serie: due elementi circuitali sono in serie se sono attraversati dalla stessa corrente. Nota Bene: in questo contesto “stessa corrente” non vuol dire “stesso valore di corrente”, ma che tutte le cariche che passano attraverso uno degli elementi attraversano anche l’altro.

Nel caso dei resistori, consideriamone due in serie (di resistenza $R_1$ ed $R_2$) ed applichiamo la legge di Ohm ad entrambi, tenendo conto che la corrente che scorre al loro interno è la stessa:

$$ \begin{align} \Delta V_1 & = R_1 i\\ \Delta V_2 & = R_2 i \end{align} $$

Quindi la differenza di potenziali ai capi del resistore equivalente vale

$$ \Delta V = \Delta V_1 + \Delta V_2 = (R_1 + R_2) i $$

Questo stesso ragionamento si generalizza al caso di $N$ resistori: la resistenza equivalente di resistori in serie è la somma delle singole resistenze.

Resistori in parallelo

Elementi connessi in parallelo hanno la stessa differenza di potenziale $\Delta V$, ma sono attraversati da correnti diverse. D’altro canto, la condizione di stazionarietà implica che la somma di queste correnti sia la stessa da entrambi i lati della connessione.

Facciamo il caso di due resistori $R_1$ ed $R_2$, per cui si ha:

\begin{align} \Delta V & = R_1 i_1\\ \Delta V & = R_2 i_2 \end{align}

Imponendo $i = i_1 + i_2$ (cioè la condizione di stazionarietà appena discussa) si ottiene

$$ i = \left( \frac{1}{R_1} + \frac{1}{R_2} \right) \Delta V $$

La stessa relazione si ottiene considerando un sistema di $N$ resistori in parallelo: la resistenza equivalente di resistori in parallelo è l’inverso della somma delle singole resistenze inverse.

Carica di un condensatore

Consideriamo un circuito composto da un generatore di forza elettromotrice $\mathcal{E}$, una resistenza $R$ ed un condensatore $C$. La resistenza interna del generatore può essere considerata trascurabile (o inclusa in $R$). Il circuito è inizialmente aperto. Al tempo $t = 0$ il collegamento viene chiuso. Come variano nel tempo la corrente $i(t)$, le d.d.p. ai capi degli elementi del circuito, $\Delta V_R(t)$ e $\Delta V_C(t)$, e la carica immagazzinata sul condensatore $q(t)$?

Consideriamo il sistema stazionario: la corrente che scorre nel circuito varia nel tempo, ma ad un dato istante $t$ l’intensità di corrente è la stessa ovunque. In un istante generico $t$ si deve quindi avere

\begin{align} \Delta V_C(t) & = \frac{q(t)}{C}\\ \Delta V_R(t) & = R i(t) = R \frac{dq}{dt}\\ \mathcal{E} & = \Delta V_C(t) + \Delta V_R(t) \end{align}

Si ha quindi

$$ R \frac{dq}{dt} = \mathcal{E} - \frac{q}{C} $$

Questa è, dal punto di vista matematico, un’equazione differenziale, cioè un’equazione in cui “l’incognita” è una funzione piuttosto che un numero (in questo caso la funzione $q(t)$). Le equazioni differenziali di questo tipo sono facilmente risolvibili per separazione di variabili. Riscriviamo l’equazione mettendo in un membro tutto ciò che dipende dall’argomento della funzione ($t$) e nell’altro tutto ciò che è legato alla funzione:

$$ \frac{dq}{C\mathcal{E} - q} = \frac{dt}{RC} $$

Integriamo entrambi i membri da $0$ a $t$ imponendo la condizione iniziale $q(0) = 0$:

$$ \int_0^q \frac{dq’}{C\mathcal{E} - q’} = -\left( \log{(C\mathcal{E} - q)} - \log{(C\mathcal{E})} \right) = -\log{\left( \frac{C\mathcal{E} - q}{C\mathcal{E}} \right) } $$

$$ \int_0^t \frac{dt’}{RC} = \frac{t}{RC} $$

Spostando il segno $-$ dal membro di sinistra a quello di destra ed esponenziandoli entrambi si ottiene

$$ C\mathcal{E} - q = C\mathcal{E}e^{-\frac{t}{RC}} $$

Da cui si ricava:

$$ q(t) = C\mathcal{E} \left( 1 - e^{-\frac{t}{RC}} \right) $$

Sostituendo questa relazione nelle precedenti troviamo:

$$ \begin{align} i(t) &= \frac{\mathcal{E}}{R}e^{-\frac{t}{RC}}\\ \Delta V_C & = \mathcal{E} \left( 1 - e^{-\frac{t}{RC}} \right)\\ \Delta V_R & = \mathcal{E} e^{-\frac{t}{RC}} \end{align} $$

Tutte le quantità variano in maniera esponenziale, con il tempo caratteristico dato dal prodotto $RC$ (che infatti si misura in secondi). Tutte le quantità finali sono quindi raggiunte asintoticamente (ma dal punto di vista pratico questo avviene quando $t \gtrsim 5 RC$). Se variamo i componenti in maniera che questo prodotto rimanga invariato, la dipendenza dal tempo di tutte le quantità rimane costante. Cambiano però i valori finali (che dipendono da $\mathcal{E}$ e da $C$ o $R$, mai da entrambi). L’interpretazione di questi risultati è semplice: la corrente è massima all’inizio, quando la carica è nulla. Mano a mano che il condensatore si carica la corrente diminuisce, la d.d.p. ai capi del condensatore aumenta (con $q$), mentre quella ai capi del resistore diminuisce.

Se chiamiamo $q_f = \mathcal{E}C$ il valore di carica asintotico, il lavoro compiuto dal generatore per caricare il condensatore vale:

$$ W_g = \int_0^{q_f} \mathcal{E} dq = \mathcal{E} q_f = \mathcal{E}^2 C $$

D’altro canto, l’energia elettrostatica immagazzinata dal condensatore è:

$$ \frac{1}{2} q_f \mathcal{E} = \frac{1}{2} \mathcal{E}^2 C $$

cioè metà dell’energia spesa dal generatore. Il resto viene dissipato sulla resistenza. La potenza totale erogata, quindi, viene consumata sulla resistenza per effetto Joule e per aumentare l’energia elettrostatica del condensatore, caricandolo. Utilizzando le relazioni ottenute precedentemente si può trovare che, ad ogni istante, vale la relazione:

$$ \mathcal{P}_g = \mathcal{P}_R + \mathcal{P}_C $$

Scarica di un condensatore

Consideriamo un circuito aperto formato da un condensatore $C$, inizialmente carico con carica $q_0$, e da una resistenza $R$. Calcoliamo come variano nel tempo le quantità introdotte nel paragrafo precedente se il circuito viene chiuso.

Le espressioni per la d.d.p. ai capi dei due elementi sono le stesse del caso precedente:

$$ \Delta V_R = R i(t) = R \frac{dq}{dt} $$

$$ \Delta V_C = \frac{q(t)}{C} $$

anche se in questo caso non è presente alcun generatore, quindi

$$ \Delta V_R + \Delta V_C = R \frac{dq}{dt} + \frac{q(t)}{C} = 0 $$

che è di nuovo un’equazione differenziale risolvibile per separazione di variabili:

$$ \frac{dq}{q} = -\frac{dt}{RC} $$

che integriamo di nuovo da 0 a $t$, con condizione iniziale $q(0) = q_0$, ottenendo

$$ \begin{align} q(t) & = q_0 e^{-\frac{t}{RC}}\\ i(t) & = -\frac{q_0}{RC} e^{-\frac{t}{RC}}\\ \Delta V_C & = \frac{q_0}{C} e^{-\frac{t}{RC}}\\ \Delta V_R & = -\frac{q_0}{C} e^{-\frac{t}{RC}} \end{align} $$

Nota Bene: la corrente ha segno negativo, perché la carica sta diminuendo, quindi $dq/dt < 0$. La dipendenza temporale è identica a prima, essendo caratterizzata unicamente dal prodotto $RC$. In questo caso si parte da una condizione di carica massima del condensatore, che ha inizialmente energia $U_e = \frac{q_0^2}{2 C}$. Alla fine del processo (cioè per $t \to \infty$) la carica è nulla e quindi $U_e = 0$. Dove è finita l’energia? Calcoliamo la potenza istantanea dissipata sul resistore:

$$ \mathcal{P}_R(t) = R i^2 = \frac{q_0^2}{RC^2} e^{-2\frac{t}{RC}} $$

L’energia totale dissipata in un tempo $t$ è l’integrale della potenza da $0$ a $t$, che per $t \to \infty$ vale

$$ W_R = \int_0^\infty \frac{q_0^2}{RC^2} e^{-2\frac{t’}{RC}} dt’ = \frac{q_0^2}{2 C} $$

Prima legge di Kirchhoff

In virtù del principio di conservazione della carica, possiamo generalizzare il principio di stazionarietà ad un nodo da cui escano $N$ rami, ognuno dei quali percorso da una corrente $i_k$:

$$ \sum_{k = 0}^N i_k = 0 $$

anche detta prima legge di Kirchhoff. Quando si applica questa legge bisogna fare attenzione al verso delle correnti, che va preso con segno diverso a seconda che queste siano entranti o uscenti.

Seconda legge di Kirchhoff

In base alle definizioni del paragrafo precedente, in ogni ramo di un circuito scorre una corrente $i_k$. Questa corrente può essere sia positiva che negativa, a seconda del verso in cui scorre. Su un ramo generico, che connette i nodi $A$ e $B$, vale la legge generalizzata di Ohm:

$$ V_A - V_B + \mathcal{E}_r + \Delta V_r^{(C )} = R_r i_k $$

dove il primo termine è la differenza di potenziale tra i due nodi, il secondo è la somma delle forze elettromotrici presenti lungo il ramo, il terzo è dato dalle d.d.p. di elementi che non sono né resistori né generatori (come i condensatori), e $R_r$ è la resistenza totale del ramo. Se consideriamo ora una maglia della rete, possiamo sommare le leggi di Ohm generalizzate per ognuno dei rami che la compongono. Per farlo è necessario prima di tutto fissare, per convenzione, il verso con cui si percorre la maglia (ad esempio: orario o antiorario). In questo modo la somma delle d.d.p. lungo la maglia si annulla e quindi si ottiene:

$$ \sum_k \mathcal{E}_k + \sum_k \Delta V_k^{(C )} = \sum_k R_k i_k $$

dove le somme sono estese a tutti i rami $k$ della maglia. Se sono presenti solo generatori e resistori, la relazione precedente si riduce a:

$$ \sum_k \mathcal{E}_k = \sum_k R_k i_k. $$

Questa equazione è chiamata seconda legge di Kirchhoff. Per applicare questa legge bisogna prima di tutto, come detto, fissare un verso di percorrenza. Dato un verso, la forza elettromotrice di generatori che sono orientati in maniera tale da avere prima il morsetto negativo e poi quello positivo danno contributo positivo (e viceversa). Similmente, correnti parallele al verso scelto sono positive (e viceversa).

Per reti elettrici generiche bisogna scrivere un’equazione per ogni maglia (applicando la seconda legge di Kirchoff) e un’equazione per ogni nodo (applicando la prima legge di Kirchoff). Per trovare le correnti (o le quantità incognite) bisogna quindi risolvere il sistema di equazioni risultante.

Un esempio

Calcoliamo le correnti che scorrono nel circuito in figura

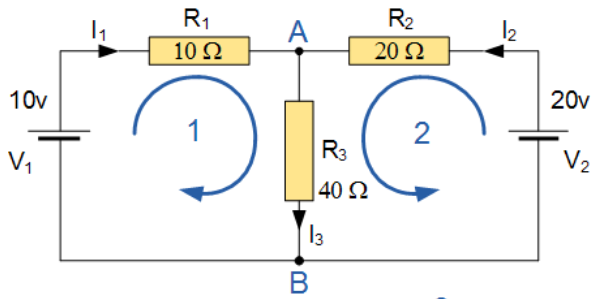
Scegliamo arbitrariamente i versi delle correnti in maniera tale che nelle due maglie (1 e 2) si vada dal polo positivo a quello negativo di ogni generatore. Applichiamo la prima legge di Kirchhoff nel nodo $A$:

$$ i_1 + i_2 = i_3. $$

Per le due maglie, invece, vale

\begin{align} V_1 & = i_1 R_1 + i_3 R_3\\ V_2 & = i_2 R_2 + i_3 R_3 \end{align}

Le equazioni si risolvono sostituendo la prima nelle ultime due e poi isolando le due correnti. Nello specifico caso in esame si trova $i_1 = -0.143$ A, $i_2 = 0.429$ A e $i_3 = 0.286$ A. Il fatto che $i_1$ sia negativa significa che il suo verso è contrario a quello che abbiamo scelto per applicare le leggi di Kirchoff.