Coordinate cartesiane

Durante il corso utilizzeremo quasi sempre le coordinate cartesiane. In questo sistema, un punto nello spazio è identificato da tre numeri che rappresentano le coordinate di quel punto lungo gli assi $x$, $y$ e $z$. Due possibili notazioni per scrivere lo stesso vettore di componenti $a$, $b$ e $c$ sono $(a, b, c$) oppure $a\hat{x} + b\hat{y} + c\hat{z}$, dove i tre versori indicano le tre direzioni cartesiane, cioè:

$$ \hat{x} = (1, 0, 0), \hat{y} = (0, 1, 0), \hat{z} = (0, 0, 1) $$

Questi versori (e la loro somma pesata, che può generare qualunque altro vettore nello spazio) non hanno nulla di speciale, e si trattano esattamente come ogni altro vettore. In effetti, le coordinate di un generico vettore $\vec{v} = (v_x, v_y, v_z)$ lungo i tre assi cartesiani si possono trovare applicando il prodotto scalare ai tre versori. Facciamo un esempio con la componente $\hat{x}$:

$$ \vec{v} \cdot \hat{x} = (v_x\hat{x} + v_y\hat{y} + v_z\hat{z}) \cdot \hat{x} = v_x $$

perché $\hat{x}$, $\hat{y}$ e $\hat{z}$ sono ortogonali fra di loro!

Sistemi di riferimento

Attenzione: il sistema di riferimento che scegliamo di utilizzare è una costruzione artificiale (umana, se volete) e quindi non può avere nessun effetto sul fenomeno fisico che intendiamo osservare/studiare. Infatti, i fenomeni fisici sono indipendenti dal modo in cui li studiamo, ma le equazioni che li descrivono no: scegliere un “buon” sistema di riferimento può semplificare grandemente i calcoli.

Esercizi svolti in aula

• Quanto fa $\hat{x} \cdot \hat{y}$? Perché?

  • Risposta: 0, perché sono ortogonali

• Quanto vale l’angolo compreso tra $\vec{v} = 3 \hat{x} + 3 \hat{y}$ e $\vec{w} = 2\hat{x} + \hat{y}$?

  • Risposta: $18.49^\circ$, cioè $0.32$ rad

• Quanto vale il modulo del vettore $\vec{v} = \hat{x} + 4 \hat{y} - 2\sqrt{2} \hat{z}$? E qual è l’espressione di $\hat{v}$?

  • Risposte: $5$ e $\hat{v} = \frac{1}{5} \hat{x} + \frac{4}{5} \hat{y} - \frac{2\sqrt{2}}{5} \hat{z}$

• Un vettore $\vec{v} = v_x \hat{x} + v_y \hat{y}$ di modulo $4$ giace sul piano $(x, y)$ e forma un angolo di $\pi/3$ con l’asse $x$. Quali sono le sue componenti?

  • Risposta: definendo $v$ il modulo si trova $v_x = v \cos(\theta) = 2.00$, $v_y = v \sin(\theta) = 3.46$

• Dati due punti $A = (1, 2, 0)$ e $B = (6, 3, 0)$, determinare

  • il vettore che congiunge $A$ a $B$

    • $\vec{v} = (6, 3, 0) - (1, 2, 0) = (5, 1, 0)$;

  • la distanza tra $A$ e $B$

    • questa sarà il modulo del vettore, $v = \sqrt{26}$;

  • il versore che punta da $A$ a $B$

    • il versore è definito come $\vec{v} / v = \frac{1}{\sqrt{26}}(5, 1, 0)$

  • il versore che punta da $B$ ad $A$

    • questo versore è uguale a quello sopra cambiato di segno. Perché?

• Dati due vettori $\vec{a} = (2, 3, 0)$ e $\vec{b} = (-2, h, 0)$, quanto deve valere $h$ affinché i vettori risultino perpendicolari? E affinché risultino (anti)paralleli (non fate i conti, delinate solamente la strategia da utilizzare, per esempio disegnando i due vettori)?

  • Risposte: imponendo $\vec{a} \cdot \vec{b} = -4 + 3h + 0 = 0$ si trova $h = 4/3$. La seconda risposta è un po’ più complicata, ma si affronta considerando che la condizione di parallelismo si può scrivere come $\cos\theta = \frac{\vec{a} \cdot \vec{b}}{ab} = \pm 1$. Se disegniamo i due vettori vedremo che l’unica possibilità che abbiamo è di imporre $\cos{\theta} = -1$, che si ottiene solo se $h = -3$, cioè quando $\vec{a} = -\vec{b}$!

Esercizi per casa

• Un aereo percorre 100 Km in direzione nord, per poi virare e percorrere 150 Km in direzione nord $30^\circ$ est ed infine percorrere 300 Km in direzione est. Calcolare lo spostamento risultante in modulo, direzione e verso.

  • Risposta: il primo vettore (omettendo le unità di misura per comodità, ma è tutto misurato in Km) vale $\vec{s}_1 = (0, 100)$, $\vec{s}_2 = (75, 75 \sqrt{3})$ e $\vec{s}_3 = (300, 0)$. Il vettore spostamento totale è quindi $\vec{s}_t = (375, 100 + 75 \sqrt{3}) = (375, 229.9)$, e il suo modulo vale $s = \sqrt{375^2 + 229.9^2} = 439.86$ Km. Per quanto riguarda la direzione, il vettore forma un angolo $\alpha$ con l’asse $x$ che è dato da $s \cos\alpha = s_x$ e quindi $\alpha = \arccos\left(\frac{s_x}{s}\right) = 0.55 , {\rm rad} = 31.5^\circ$.

• Un giocatore di golf in tre colpi riesce a gettare la sua palla nella buca. Il primo tiro sposta la palla di 12 m a nord, il secondo di 6 m a sud–est (cioè con un angolo $-\pi/4 = -45^\circ$) ed il terzo tiro di 3 m a sud–ovest (cioè con un angolo $-3\pi/4 = -135^\circ$). Quale spostamento è necessario per mandare la palla nella buca al primo colpo?

  • Ragionando come sopra otteniamo $s = 6$ m e $\alpha = 1.21 , {\rm rad} = 69.4^\circ$.

Coordinate sferiche

Le coordinate sferiche $(r, \theta, \phi)$ sono legate a quelle cartesiane, $(x, y, z)$, tramite le seguenti relazioni:

$$ \left\lbrace \begin{aligned} x &= r \sin(\theta) \cos(\phi)\\ y &= r \sin(\theta) \sin(\phi)\\ z &= r \cos(\theta) \end{aligned} \right. $$

Il seguente diagramma aiuta a visualizzare queste relazioni:

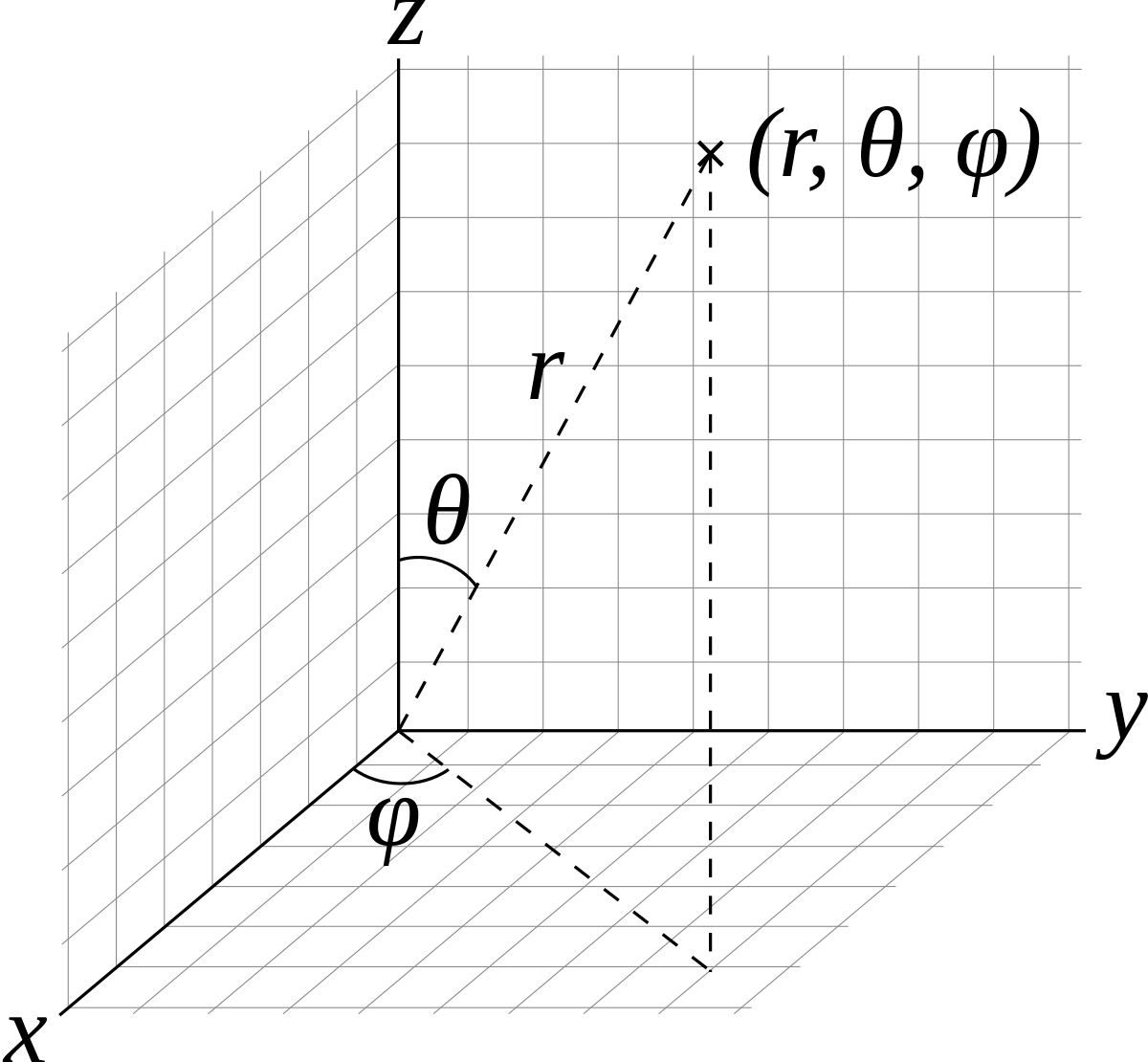
In generale, nei sistemi di riferimento che ci interessano i versori che indicano le direzioni delle coordinate sono sempre ortogonali tra loro, punto per punto. Nel caso delle coordinate cartesiane questi vettori sono sempre uguali e puntano sempre nella stessa direzione. Nel caso delle coordinate sferiche questo non è vero: mentre, punto per punto, i tre versori sono ortogonali, le loro direzioni dipendono dal punto in cui vogliamo calcolarli. Per trovarli bisogna disegnare il punto in cui siamo su di un diagramma simile a quello riprodotto sopra e chiedersi quali sono le direzioni verso le quali le tre coordinate aumentano. Nel caso del punto in figura (indicato con $\times$):

• $\hat{r}$ ha direzione parallela a quella della linea tratteggiata che connette $\times$ all’origine e verso che allontana dall’origine

• $\hat{\theta}$ ha la direzione che lascia inalterati $r$ e $\phi$ e verso che fa crescere $\theta$.

• $\hat{\phi}$ fa ruotare in senso antiorario il punto attorno all’asse $z$.

Coordinate polari

Il discorso si semplica in 2D, dove si hanno solamente $r$ e $\theta$:

$$ \left\lbrace \begin{aligned} x &= r \cos(\theta)\\ y &= r \sin(\theta) \end{aligned} \right. $$

Tramite queste relazioni possiamo ottenere le coordinate di un vettore conoscendo il suo modulo (cioè $r$) e l’angolo che forma con l’asse $x$.

Derivate

Data una funzione $f(x)$, la sua derivata $\frac{df(x)}{dx}$ misura quanto $f(x)$ cambi al variare di $x$. In pratica, la derivata di $f(x)$ calcolata nel punto $x_0$ è la pendenza della tangente di $f(x_0)$.

Il concetto di derivata si può estendere anche a funzioni multidimensionali tramite la nozione di derivata parziale, che misura come una funzione di più variabili vari lungo una particolare direzione (per esempio $x$, $y$ o $z$). La derivata parziale di $f(x, y)$ rispetto ad $x$ si scrive $\frac{\partial}{\partial x} f(x, y)$. Dal punto di vista operativo, una derivata parziale si effettua in maniera del tutto analoga ad una derivata normale, avendo l’accortezza di considerare costanti le variabili su cui non si deriva.

Alcune relazioni utili legate alle derivate (a, b e c sono scalari):

• $\frac{d}{dx} (ax^b + c) = abx^{b-1}$

• $\frac{d}{dx} e^{ax} = ae^{ax}$

• $\frac{d}{dx} \cos(ax) = -a\sin(ax)$

• $\frac{d}{dx} \sin(ax) = a\cos(ax)$

• $\frac{d}{dx} \log(ax) = \frac{1}{x}$

• $\frac{d}{dx} (f(x)g(x)) = \frac{df(x)}{dx}g(x) + f(x)\frac{dg(x)}{dx}$

• $\frac{d}{dx} f(g(x)) = \frac{df(g(x))}{dg(x)}\frac{dg(x)}{dx}$

• $\frac{\partial}{\partial x} (ax^2y + y) = 2ax$

Integrali

Per quel che concerne l’argomento del corso, l’integrale può essere visto come una somma di tanti (infiniti) contributi molto piccoli (infinitesimi). Integrali e derivate sono intimamente connessi tramite il cosiddetto teorema fondamentale del calcolo integrale. Questo afferma che, data una funzione $f(x)$ continua in un intervallo $(a, b)$, si può scrivere (in quello stesso intervallo)

$$F(x) = \int_a^x f(x’) dx’,$$

dove $\frac{dF(x)}{dx} = f(x)$. Integrali e derivate sono quindi operazioni inverse. Nel caso di estremi di integrazione costanti si ha che, se $\frac{df(x)}{dx} = g(x)$, allora $\int_a^b g(x) dx = f(b) - f(a)$.

Nota Bene: poiché la derivata di una costante è 0, se $\frac{dF(x)}{dx} = f(x)$ e $G(x) = F(x) + C$ con $C$ costante, si avrà $\frac{dG(x)}{dx} = f(x)$.

In maniera del tutto analoga a quanto fatto per le derivate, anche il concetto di integrale può essere esteso a funzioni multidimensionali.

Una distinzione fondamentale è quella tra gli integrali indefiniti e quelli definiti:

• In un integrale indefinito le variabili figurano negli estremi di integrazione o non figurano affatto. Il risultato di un’integrazione indefinita di una funzione a $N$ variabili è anch’esso una funzione ad $N$ variabili. Si scrive quindi (impropriamente o, come i matematici amano dire, con un abuso di notazione) $g(x) = \int f(x) dx$.

• Un integrale definito ha come estremi di integrazione delle costanti. Il tipo di risultato dipende dal numero di variabili su cui si integra: un integrale doppio di una funzione a due variabili è uno scalare, mentre un integrale singolo della stessa funzione a due variabili è una funzione di una variabile.

Alcuni esempi:

• $$\int ax^bdx = \frac{ax^{b+1}}{b+1} \qquad\textrm{(per $b\neq -1$, perché?)}$$

• $$\int \cos(ax) dx = \frac{\sin(ax)}{a}$$

• $$\int_0^2 (x^2 + 1)dx = \left.\left( \frac{1}{3}x^3 + x\right)\right|_0^2 = \frac{14}{3}$$

• $$\int_0^\pi \cos^2(ax) dx = \frac{\pi}{2}$$

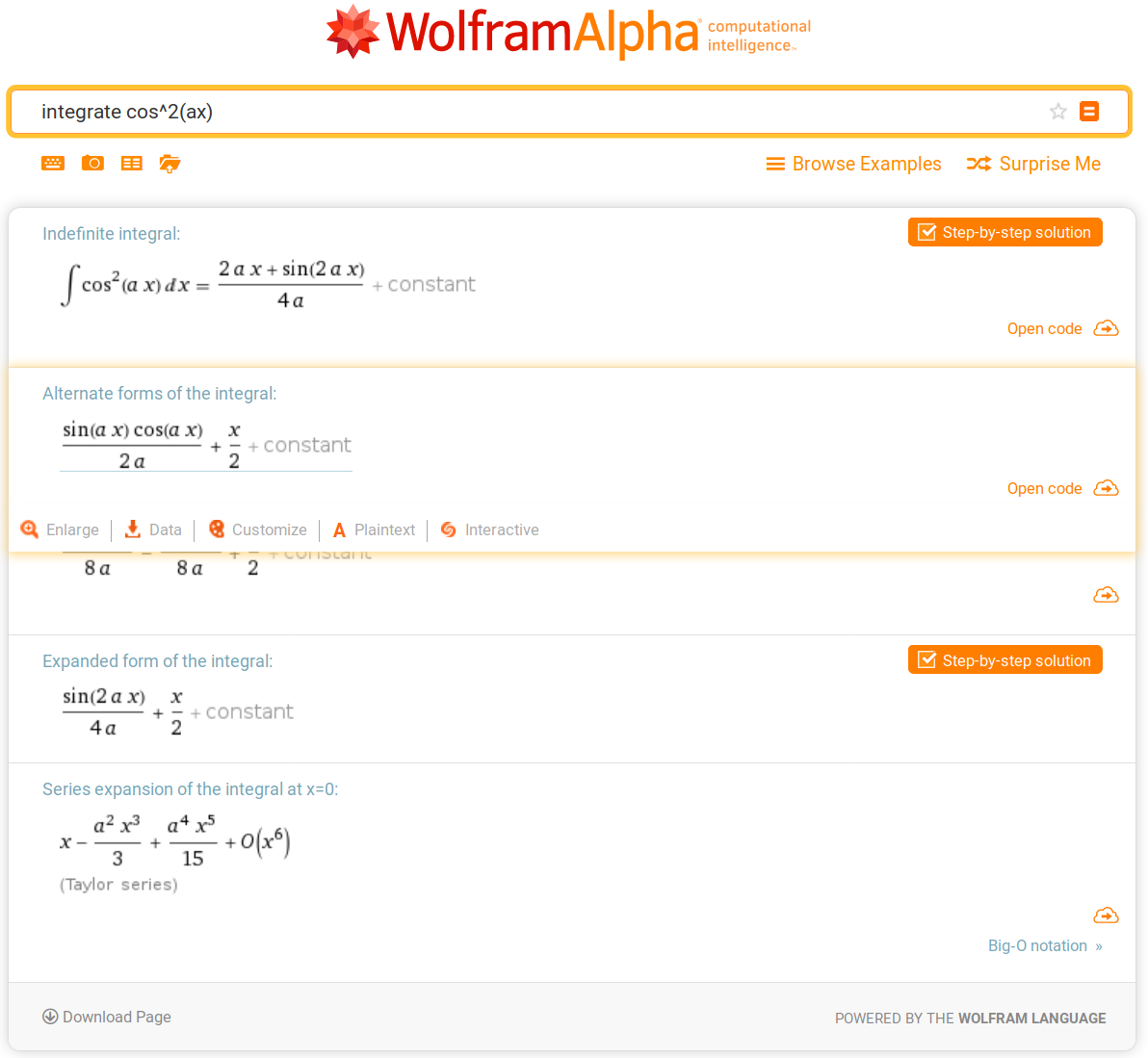
Durante il corso spiegherò tutti i passaggi degli integrali che incontreremo. Tenete conto che integrare è difficile, quindi non preoccupatevi se incontrerete difficoltà. In ogni caso, per calcolare integrali generici si può utilizzare il sito di Wolfram Alpha come nell’immagine che segue:

Integrali in coordinate sferiche e polari

Troviamo ora le relazioni che legano l’incremento della coordinata $i$-esima allo spostamento $ds_i$ che ne risulta. Per le coordinate cartesiane questo è semplicemente dato da $ds_x = dx$, $ds_y = dy$ e $ds_z = dz$. Per le coordinate sferiche, invece:

• Se ci si muove lungo $\hat{r}$, $r$ aumenta e $\times$ si sposta di una quantità pari all’incremento. Si ha quindi uno spostamento pari a $ds_r = dr$.

• Se ci si muove lungo $\hat{\theta}$ di un angolo $d\theta$, lo spostamento sarà pari a $ds_\theta = 2 r \sin(d\theta / 2) \approx r d\theta$, dove abbiamo utilizzato il fatto che $\sin (\alpha) \approx \alpha$ per piccoli valori di $\alpha$.

• Se ci si muove lungo $\hat{\phi}$, per visualizzare lo spostamento prima proiettiamo il punto sul piano $x-y$ (contribuendo con un fattore $\sin(\theta)$) e poi effettuiamo la stessa operazione del punto precedente, ma stavolta utilizzando $d\phi$. Il risultato finale è quindi $ds_\phi = r \sin(\theta) d\phi$.

Possiamo usare queste relazioni per ottenere l’espressione di un volumetto infinitesimo $d\tau = ds_1 ds_2 ds_3$:

• In coordinate cartesiane $d\tau = dx dy dz$.

• In coordinate sferiche $d\tau = ds_r ds_\theta ds_\phi = r^2 \sin(\theta) dr d\theta d\phi$.

L’espressione si semplifica in casi specifici:

• se l’integrando non dipende da $\theta$, $d\tau = 2 r^2 dr d\phi$;

• se l’integrando non dipende da $\phi$, $d\tau = 2 \pi r^2 \sin(\theta) dr d\theta$;

• se l’integrando non dipende né da $\theta$ né da $\phi$, $d\tau = 4\pi r^2 dr$.

Per gli spostamenti infinitesimi in coordinate polari:

• Se ci si muove lungo $\hat{r}$, $r$ aumenta e $\times$ si sposta di una quantità pari all’incremento. Si ha quindi uno spostamento pari a $ds_r = dr$.

• Se ci si muove lungo $\hat{\theta}$ di un angolo $d\theta$, lo spostamento sarà pari a $ds_\theta = 2 r \sin(d\theta / 2) \approx r d\theta$, dove abbiamo utilizzato il fatto che $\sin (\alpha) \approx \alpha$ per piccoli valori di $\alpha$.

L’espressione di una porzione infinitesimo della superficie è quindi $d\Sigma = dx dy = r dr d\theta$. Se l’integrando non dipende da $\theta$ si ha $d\Sigma = 2 \pi r dr$.

Esercizi

1. $3 \times 10^{-3} \frac{10^6}{10^{-4}} =$ ?

2. $\frac{10^{-9}}{8.854 \times 10^{-12}} 10^{-2} =$ ?

3. Se $a = 1$ s, $b = 1$ m e $c = 1$ m/s, si può scrivere $a/b + c$? E $ac + b$?

4. Se $a = 1$ m$^{-1}$ e $b = 10$ cm$^{-1}$, quanto fa $a + b$?

5. $600$ cm$^3 = \ldots$ m$^3$

6. $0.0009$ Km$^3 = \ldots$ m$^3$

Risposte:

1. $3 \times 10^7$

2. $1.13$

3. No e sì

4. $1001$ m$^{-1}$

5. $6 \times 10^{-4}$ m$^3$

6. $9 \times 10^5$ m$^3$