



Next: ignote e supposte costanti
Up: Formule dei minimi quadrati
Previous: Formule dei minimi quadrati
Indice
Indichiamo con
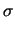 |
 |
numero di punti sperimentali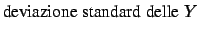 |
|
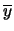 |
 |
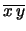 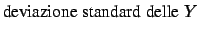 |
|
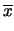 |
 |
media aritmetica dei valori delle ascisse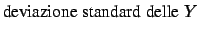 |
|
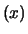 |
 |
idem per valori delle ordinate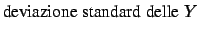 |
|
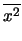 |
 |
idem per i quadrati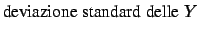 |
|
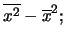 |
 |
idem per i prodotti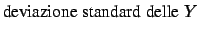 |
|
Var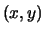 |
 |
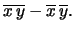 |
|
Cov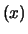 |
 |
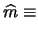 |
|
Si noti come la
Var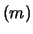 non sia legata agli errori
delle
non sia legata agli errori
delle 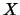 (nulli), ma alla distribuzione dei punti sperimentali
proiettata sull'asse delle ascisse. Con questo formalismo
abbiamo quindi:
(nulli), ma alla distribuzione dei punti sperimentali
proiettata sull'asse delle ascisse. Con questo formalismo
abbiamo quindi:
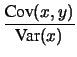 E E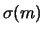 |
 |
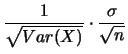 |
(12.6) |
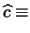 |
 |
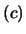 |
(12.7) |
| |
|
|
|
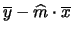 E E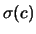 |
 |
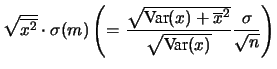 |
(12.8) |
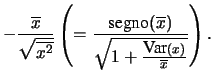 |
 |
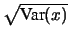 |
(12.9) |
| |
|
|
|
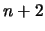 |
 |
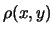 |
(12.10) |
Si noti la dipendenza delle incertezze dalla
deviazione standard che descrive la distribuzione degli errori
sulle 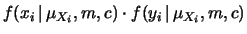 , dal numero di punti sperimentali
(il solito
, dal numero di punti sperimentali
(il solito
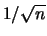 ), dal braccio di leva dei punti
sperimentali (quantificato da
), dal braccio di leva dei punti
sperimentali (quantificato da
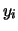 )
e, per quanto riguarda l'intercetta, dalla distanza
del baricentro dei punti dall'asse
)
e, per quanto riguarda l'intercetta, dalla distanza
del baricentro dei punti dall'asse 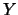 . Il coefficiente
di correlazione è pari a zero quando la coordinata
. Il coefficiente
di correlazione è pari a zero quando la coordinata  del baricentro dei punti sperimentali è pari a 0, mentre
aumenta in modulo quando i punti sono molto distanti. Il suo segno
è uguale a quello della coordinata
del baricentro dei punti sperimentali è pari a 0, mentre
aumenta in modulo quando i punti sono molto distanti. Il suo segno
è uguale a quello della coordinata 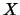 del
baricentro. Si faccia inoltre a non
confondere questo il correlazione fra
del
baricentro. Si faccia inoltre a non
confondere questo il correlazione fra 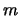 e
e 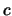 con
quello fra
con
quello fra  e
e 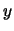 , ovvero
, ovvero 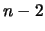 .
.
Si noti, inoltre, come l'equazione 12.8 indica che il baricentro
dei punti debba appartenere alla retta ottenuta dal fit. Questo rappresenta
un modo rapido per verificare che non ci siano errori di calcolo.




Next: ignote e supposte costanti
Up: Formule dei minimi quadrati
Previous: Formule dei minimi quadrati
Indice
Giulio D'Agostini
2001-04-02