



Next: Valutazione semplificata di
Up: Analisi grafica
Previous: Stima dell'incertezza sui parametri
Indice
Figura:
Residui e barre di incertezza (
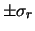 ).
).
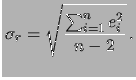 |
In realtà non c'è alcun bisogno di ripetere le serie di misure.
Se ciascuna serie contiene un numero sufficiente
di punti (tipicamente, leggermente superiore al numero di parametri
che si vogliono valutare) essa racchiude in sé le informazioni
necessarie alla valutazione delle incertezze, o almeno a quelle
derivanti da errori casuali, mediante il metodo dei residui.
Una volta tracciata la retta si può leggere dal grafico, per
ogni punto, il residuo  , ovvero la differenza fra l'ordinata
misurata e il valore della retta in corrispondenza dell'ascissa
misurata, come mostrato in figura
12.3.
Si ottiene quindi, dalla media dei quadrati dei residui,
la stima della deviazione standard delle ordinate, assumendo
che sia la stessa per tutti i punti e attribuendo soltanto
alle ordinate le deviazioni dal valore vero:
Il nome
, ovvero la differenza fra l'ordinata
misurata e il valore della retta in corrispondenza dell'ascissa
misurata, come mostrato in figura
12.3.
Si ottiene quindi, dalla media dei quadrati dei residui,
la stima della deviazione standard delle ordinate, assumendo
che sia la stessa per tutti i punti e attribuendo soltanto
alle ordinate le deviazioni dal valore vero:
Il nome  sta a indicare
sia che essa è calcolato dai residui sia
che rappresenta l'equivalente
della deviazione standard di ripetitività delle misure.
Il fattore
sta a indicare
sia che essa è calcolato dai residui sia
che rappresenta l'equivalente
della deviazione standard di ripetitività delle misure.
Il fattore 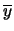 al posto di
al posto di  ha la stessa giustificazione
dell'
ha la stessa giustificazione
dell'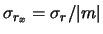 nella deviazione standard, tenendo conto che ora ci sono
due vincoli fra i dati. Ripetiamo ancora una volta quanto detto
a proposito di
nella deviazione standard, tenendo conto che ora ci sono
due vincoli fra i dati. Ripetiamo ancora una volta quanto detto
a proposito di
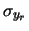 : anche se le ragioni profonde
di questa scelta non sono sempre condivisibili, il risultato
``va nella direzione giusta''. Anche qui, quando
: anche se le ragioni profonde
di questa scelta non sono sempre condivisibili, il risultato
``va nella direzione giusta''. Anche qui, quando  è dell'ordine
della decina, la correzione è ininfluente ai fini pratici.
è dell'ordine
della decina, la correzione è ininfluente ai fini pratici.
A questo punto, finalmente si conosce l'errore casuale
sulle ordinate
in condizioni di ripetività (nell'ipotesi
che quello sulle ascisse sia trascurabile)!
Ovviamente, si può anche
fare l'esercizio opposto e attribuire tutto l'errore alle ascisse
(senza dover fare tutti i conti, si può propagare 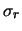 su ``
su ``
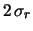 '' mediante la derivata:
'' mediante la derivata:
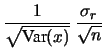 ).
È interessante notare che, anche se il punto di vista cambia
drasticamente, saranno invarianti le conclusioni
sulle grandezze fisiche di interesse, legate a coefficiente
angolare e intercetta.
).
È interessante notare che, anche se il punto di vista cambia
drasticamente, saranno invarianti le conclusioni
sulle grandezze fisiche di interesse, legate a coefficiente
angolare e intercetta.




Next: Valutazione semplificata di
Up: Analisi grafica
Previous: Stima dell'incertezza sui parametri
Indice
Giulio D'Agostini
2001-04-02
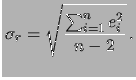
![]() su ``
su ``
![]() '' mediante la derivata:
'' mediante la derivata:
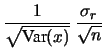 ).
È interessante notare che, anche se il punto di vista cambia
drasticamente, saranno invarianti le conclusioni
sulle grandezze fisiche di interesse, legate a coefficiente
angolare e intercetta.
).
È interessante notare che, anche se il punto di vista cambia
drasticamente, saranno invarianti le conclusioni
sulle grandezze fisiche di interesse, legate a coefficiente
angolare e intercetta.