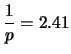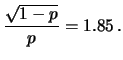Next: Numeri ritardatari al lotto
Up: Previsioni dei risultati
Previous: pzd100Contatore e distribuzione Gamma
Indice
Consideriamo di nuovo l'esperimento del contatore
per un tempo di misura pari a
 s.
La probabilità di osservare almeno un conteggio
è data da
Interessiamoci ora al seguente problema: ``quante misure bisogna
effettuare prima di osservare un conteggio?''.
In altre parole, siamo interessati numero d'ordine
(indicato con
s.
La probabilità di osservare almeno un conteggio
è data da
Interessiamoci ora al seguente problema: ``quante misure bisogna
effettuare prima di osservare un conteggio?''.
In altre parole, siamo interessati numero d'ordine
(indicato con 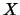 )
della misura alla quale si verifica per
la prima volta un conteggio. Date le condizioni del problema,
abbiamo che tale numero aleatorio è descritto da una
distribuzione geometrica
di parametro
)
della misura alla quale si verifica per
la prima volta un conteggio. Date le condizioni del problema,
abbiamo che tale numero aleatorio è descritto da una
distribuzione geometrica
di parametro 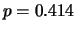 , avente valore atteso e deviazione standard
pari a
, avente valore atteso e deviazione standard
pari a
Ricordiamo che tale distribuzione si estende per valori di 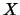 da 1 a infinito ed è quindi molto asimmetrica. Ne segue che
valori che eccedono il valore atteso
di alcune deviazioni standard sono abbastanza probabili.
Ad esempio
da 1 a infinito ed è quindi molto asimmetrica. Ne segue che
valori che eccedono il valore atteso
di alcune deviazioni standard sono abbastanza probabili.
Ad esempio
Quindi è abbastanza probabile osservare una serie di risultati
negativi (ovvero con zero conteggi) consecutivi.
All'aumentare del tempo di misura aumentano sia 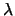 della
poissononiana che
della
poissononiana che 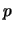 della geometrica che stiamo considerando
e quindi diventa estremamente improbabile non soltanto osservare
una lunga serie di risultati negativi, ma anche uno solo.
Ovviamente, i risultati della simulazione (vedi tabella 1.1)
confermeranno con alta probabilità le nostre aspettative.
della geometrica che stiamo considerando
e quindi diventa estremamente improbabile non soltanto osservare
una lunga serie di risultati negativi, ma anche uno solo.
Ovviamente, i risultati della simulazione (vedi tabella 1.1)
confermeranno con alta probabilità le nostre aspettative.




Next: Numeri ritardatari al lotto
Up: Previsioni dei risultati
Previous: pzd100Contatore e distribuzione Gamma
Indice
Giulio D'Agostini
2001-04-02