A curious myth is that physical probability, or propensity,
has “only a frequentist interpretation” (and therefore “physicists
must be frequentist”, as
ingenuously stated by the Roman PhD student quoted on the first page).
But it seems to me to be more a question of education, based on the
dominant school of statistics in the past century
(and presently),![[*]](footnote.png) rather than a real logical necessity.
rather than a real logical necessity.
It is a matter of fact that (relative)
frequency and probability
are somehow connected within probability theory, without the need
for identifying the two concepts.
- A future frequency
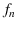 in
in 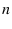 independent
`situations' (not necessarily `trials'),
independent
`situations' (not necessarily `trials'),![[*]](footnote.png) to each of which we assign probability
to each of which we assign probability 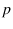 , has expected value
, has expected value
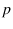 and `standard uncertainty' decreasing with increasing
and `standard uncertainty' decreasing with increasing 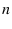 as
as
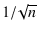 ,
though all values 0,
,
though all values 0, 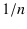 ,
, 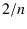 , ..., 1 are
possible (!).
This a simple result of probability theory, directly related to the
binomial distribution, that goes under the name of Bernoulli's theorem,
often misunderstood with a `limit', in
the calculus's sense. Indeed
, ..., 1 are
possible (!).
This a simple result of probability theory, directly related to the
binomial distribution, that goes under the name of Bernoulli's theorem,
often misunderstood with a `limit', in
the calculus's sense. Indeed 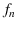 does not “tend to”
does not “tend to” 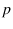 ,
but it is simply highly improbable
to observe
,
but it is simply highly improbable
to observe 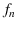 far from
far from 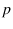 ,
for large values of
,
for large values of 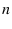 .
.![[*]](footnote.png) In particular,
under the assumption that a system
has a constant propensity
In particular,
under the assumption that a system
has a constant propensity 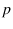 in a large number of trials,
we shall consider very “unlikely to observe
in a large number of trials,
we shall consider very “unlikely to observe 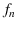 far from
far from 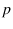 .”
.”![[*]](footnote.png) Reversing the reasoning, if we observe
a given
Reversing the reasoning, if we observe
a given 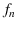 in a large number of trials, common sense
suggests that the `true
in a large number of trials, common sense
suggests that the `true 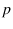 ' should lie not too far
from it, and therefore our degree of belief
in the occurrence of a future event of that kind
should be about
' should lie not too far
from it, and therefore our degree of belief
in the occurrence of a future event of that kind
should be about 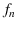 .
.
- More precisely, the probability of a future event
can be
mathematically
related, under suitable assumptions,
to the frequency of analogous
![[*]](footnote.png) events
events 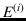 that occurred
in the past.
that occurred
in the past.![[*]](footnote.png) For example, assuming that a system has
propensity
For example, assuming that a system has
propensity 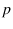 ,
after
,
after 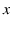 occurrences (`successes')
in
occurrences (`successes')
in 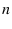 trials
we assign different beliefs to the different values of
trials
we assign different beliefs to the different values of 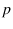 according to a probability density function
according to a probability density function 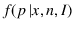 ,
whose
expression has been reported in Footnote
24.
In order to take into account all possible values of
,
whose
expression has been reported in Footnote
24.
In order to take into account all possible values of 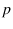 we have
to use Equation (14), in whose r.h.s. we recognize
the expected value of
we have
to use Equation (14), in whose r.h.s. we recognize
the expected value of 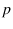 .
We get then the famous Laplace
rule of succession (and its limit for large
.
We get then the famous Laplace
rule of succession (and its limit for large 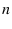 and
and 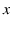 ),
),
which can be interpreted as follows. If
we i) consider the propensity of the system constant;
ii) consider all values of 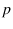 a priori equally likely
(or the weaker condition of
all values between 0 and 1 possible,
if
a priori equally likely
(or the weaker condition of
all values between 0 and 1 possible,
if 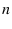 is `extraordinary large');
iii) perform a `large' number of independent trials,
then
the degree of belief we should assign to a future event
is
basically
the observed past frequency.
Equation (15)
can then be seen as a mathematical proof
that what the human mind does by intuition and
“custom” (in Hume's sense) is quite reasonable.
But the formal guidance of probability theory makes clear the
assumptions, as well as the limitations of the result.
For example, going back to our six box example, if after
is `extraordinary large');
iii) perform a `large' number of independent trials,
then
the degree of belief we should assign to a future event
is
basically
the observed past frequency.
Equation (15)
can then be seen as a mathematical proof
that what the human mind does by intuition and
“custom” (in Hume's sense) is quite reasonable.
But the formal guidance of probability theory makes clear the
assumptions, as well as the limitations of the result.
For example, going back to our six box example, if after
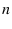 extractions we obtained
extractions we obtained 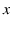 White, one could be tempted
to evaluate the probability of the next White from the observed
frequency
White, one could be tempted
to evaluate the probability of the next White from the observed
frequency 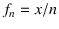 ,
instead of, as probability theory teaches,
firstly evaluating the probabilities
of the various compositions from Equation (6)
and then the probability of White from (10).
The results will not be the same and the latter
is amazingly `better'
,
instead of, as probability theory teaches,
firstly evaluating the probabilities
of the various compositions from Equation (6)
and then the probability of White from (10).
The results will not be the same and the latter
is amazingly `better'![[*]](footnote.png) (1).
(1).
There is another argument against the myth that
physical probability is `defined' via the long-term
frequency behavior. If propensity 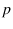 can be seen as a
parameter of a physical system, like a mass or the radius
of the sphere associated with the shape of an object, then, as other
parameters, it might change with time too,
i.e. in general we deal with
can be seen as a
parameter of a physical system, like a mass or the radius
of the sphere associated with the shape of an object, then, as other
parameters, it might change with time too,
i.e. in general we deal with 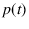 .
It is then self-evident
that different observations will refer to propensities
at different times, and there is no way to get a long-term frequency at
a given time. At most we can make sparse measurements at different
times, which could still be useful, if we have a model
of how the propensity might change with
time.
.
It is then self-evident
that different observations will refer to propensities
at different times, and there is no way to get a long-term frequency at
a given time. At most we can make sparse measurements at different
times, which could still be useful, if we have a model
of how the propensity might change with
time.![[*]](footnote.png)
![[*]](footnote.png) rather than a real logical necessity.
rather than a real logical necessity.
![[*]](footnote.png) to each of which we assign probability
to each of which we assign probability ![[*]](footnote.png) In particular,
under the assumption that a system
has a constant propensity
In particular,
under the assumption that a system
has a constant propensity ![[*]](footnote.png) Reversing the reasoning, if we observe
a given
Reversing the reasoning, if we observe
a given ![[*]](footnote.png) events
events ![[*]](footnote.png) For example, assuming that a system has
propensity
For example, assuming that a system has
propensity ![[*]](footnote.png) (1).
(1).
![[*]](footnote.png)